E. Reverse the Rivers
A conspiracy of ancient sages, who decided to redirect rivers for their own convenience, has put the world on the brink. But before implementing their grand plan, they decided to carefully think through their strategy — that's what sages do.
There are n countries, each with exactly k regions. For the j-th region of the i-th country, they calculated the value ai,j, which reflects the amount of water in it.
The sages intend to create channels between the jj-th region of the ii-th country and the jj-th region of the (i+1)-th country for all 1≤i≤(n−1) and for all 1≤j≤k.
Since all nn countries are on a large slope, water flows towards the country with the highest number. According to the sages' predictions, after the channel system is created, the new value of the j-th region of the i-th country will be bi,j=a1,j|a2,j|...|ai,j where | denotes the bitwise "OR" operation.
After the redistribution of water, the sages aim to choose the most suitable country for living, so they will send you qq queries for consideration.
Each query will contain mm requirements.
Each requirement contains three parameters: the region number r, the sign o (either "<" or ">"), and the value c. If oo = "<", then in the r-th region of the country you choose, the new value must be strictly less than the limit c, and if o = ">", it must be strictly greater.
In other words, the chosen country ii must satisfy all mm requirements. If in the current requirement o = "<", then it must hold that bi,r<c and if o = ">", then bi,r>c.
In response to each query, you should output a single integer — the number of the suitable country. If there are multiple such countries, output the smallest one. If no such country exists, output −1.
Input
The first line contains three integers nn, kk, and qq (1≤n,k,q≤1051≤n,k,q≤105) — the number of countries, regions, and queries, respectively.
Next, there are n lines, where the i-th line contains kk integers ai,1,ai,2,…,ai,k(1≤ai,j≤10^9), where ai,j is the value of the j-th region of the i-th country.
Then, q queries are described.
The first line of each query contains a single integer m (1≤m≤10^5) — the number of requirements.
Then follow m lines, each containing an integer r, a character o, and an integer c (1≤r≤k, 0≤c≤2⋅10^9), where r and c are the region number and the value, and o is either "<" or ">" — the sign.
It is guaranteed that n⋅kn⋅k does not exceed 10^5 and that the sum of mm across all queries also does not exceed 10^5.
Output
For each query, output a single integer on a new line — the smallest number of the suitable country, or −1 if no such country exists.'
题目大意
古代圣贤为了自己的方便,决定改变河流的流向,他们的阴谋将世界置于危险的边缘。但在实施他们的宏伟计划之前,他们决定仔细考虑一下他们的战略--这就是圣人的做法。
世界上有 n 个国家,每个国家正好有 k 个地区。对于 i 这个国家的 j 个地区,他们计算出了 ai,j 这个数值,它反映了其中的水量。
圣人打算在 i 国家的 j 区域和 (i+1) 国家的 j 区域之间为所有的 1≤i≤(n−1) 和所有的 1≤j≤k 修建水渠。
由于所有 nn 个国家都在一个大斜坡上,所以水会流向数字最高的国家。根据圣人的预测,通道系统建立后, i /th国家的 j /th区域的新值将是 bi,j=a1,j|a2,j|...|ai,j,其中 | 表示比特 "OR"运算。
在重新分配水源之后,圣人的目的是选择最适合居住的国家,因此他们会向你提出 q 个问题供你考虑。
每个问题都包含 m 项要求。
每个要求包含三个参数:地区编号 r 、符号 o (" <"或"> ")和值 c 。如果 o =" < ",那么在您选择的国家的 r /地区中,新值必须严格小于限值 c ;如果 o =" > ",那么新值必须严格大于限值。
换句话说,所选国家 i 必须满足所有 m 要求。如果在当前要求中 o = " < ",那么必须满足 bi,r<c ,如果 o = " > ",那么必须满足 bi,r>c。
在回答每个查询时,您应该输出一个整数--合适国家的编号。如果有多个这样的国家,则输出最小的一个。如果不存在这样的国家,则输出 −1 。
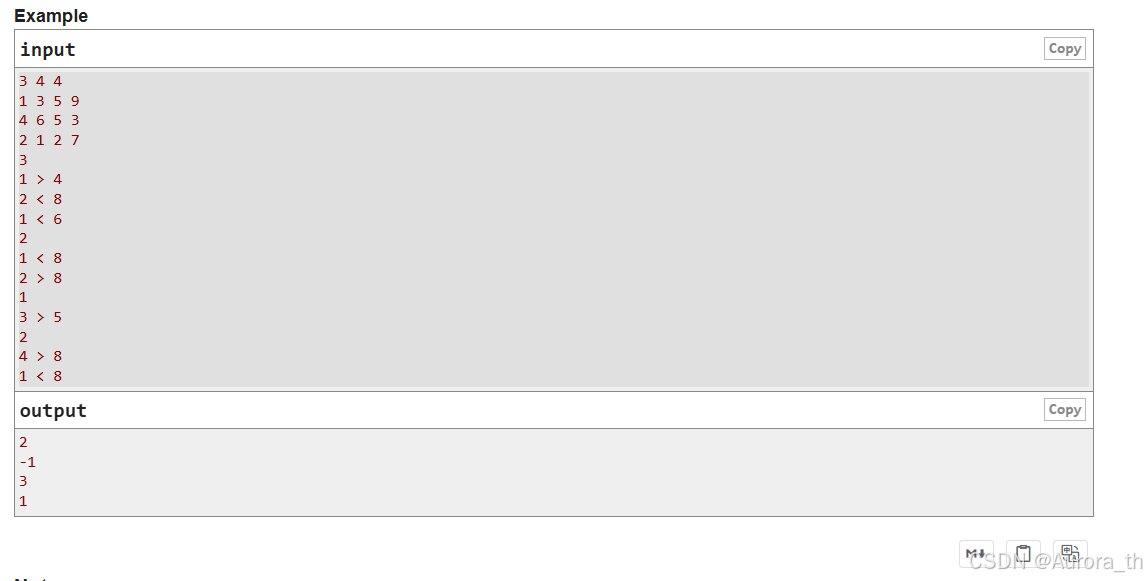

这个问题呢可以先打暴力想想思路。其实你可以发现的是只看列的话其实是单调递增的因为 | 操作之后值会越来越大。那么既然有单调性就很容易想到二分了,不过呢这道题二分要怎么写呢?你能在一次 while 循环当中找到答案吗?也许可以不过很难写,不信可以试试。
换一种思考方式,我们用二分查找来维护区间 [l, r] 也就是在这个区间的国家全部符合规定,如果l > r 那么非法输出 -1 即可,合法就输出 l
#include <iostream>
#include <vector>#define ll long longusing namespace std;int n, m, k;int main()
{cin >> n >> m >> k;vector<vector<ll>> g(n + 1, vector<ll>(m + 1, 0));for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){cin >> g[i][j];if(i > 1) g[i][j] |= g[i - 1][j];}} while(k --){int cnt;ll pos, limit;char op;int l_pos = 1, r_pos = n;cin >> cnt;while(cnt --){cin >> pos >> op >> limit;if(op == '<'){int l = 1, r = n;while(l < r){int mid = l + r + 1 >> 1;if(g[mid][pos] < limit) l = mid;else r = mid - 1;}if(g[l][pos] < limit) r_pos = min(r_pos, l);else r_pos = min(r_pos, l - 1);}else{int l = 1, r = n;while(l < r){int mid = l + r >> 1;if(g[mid][pos] <= limit) l = mid + 1;else r = mid;}if(g[l][pos] > limit) l_pos = max(l_pos, l);else l_pos = max(l_pos, l + 1);}}if(l_pos <= r_pos) cout << l_pos << endl;else cout << -1 << endl;}return 0;
}加油
