未完待续
一、质数(素数)
1.1质数的判定(试除法)
注:
(1)整除的性质:d|n,n/d|n 成对出现,n为d的整数倍
bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i <= x / i; i ++ )if (x % i == 0)return false;return true;
}1.2分解质因数(试除法)
注:n中最多只包含一个大于sqrt(n)的质因子
void divide(int x)
{//枚举到sqrt(n) for (int i = 2; i <= x / i; i ++ )if (x % i == 0){int s = 0;//枚举i的次数 while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;}//n中最多只包含一个大于sqrt(n)的质因子 if (x > 1) cout << x << ' ' << 1 << endl;cout << endl;
}1.3朴素筛法求质数(埃式筛法)
时间复杂度:O(nloglogn)

int primes[N], cnt; // primes[]存储所有素数
bool st[N];
//假设 st[]数组初始值均为 false,表示还没有任何数字被标记为合数。
// st[x]为true表示x是合数 void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (st[i]) continue;//跳过以下语句 primes[cnt ++ ] = i;for (int j = i + i; j <= n; j += i)st[j] = true;}
}1.4线性筛法求质数
n只会被最小质因子筛掉
在欧拉筛法(Euler's Sieve)中,关键点之一是确保每个合数只会被其最小质因子筛掉一次。如果继续遍历更大的素数而不跳出循环,可能会导致同一个合数被多次标记为合数,从而影响算法的效率。
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;//从小到大枚举质数 for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;//primes[j]一定是i的最小质因子 }}
}二、约数
约数(或称为因数)是指能够整除某个整数的整数。具体来说,如果整数 a能够被整数 b 整除(即 a/b的结果是整数且没有余数),那么 b 就是 a 的一个约数。
2.1试除法求所有约数
vector<int> get_divisors(int x)
{vector<int> res;//存约数 for (int i = 1; i <= x / i; i ++ )if (x % i == 0){res.push_back(i);//x有可能是i的平方,两个约数一样 if (i != x / i) res.push_back(x / i);}//给约数排序 sort(res.begin(), res.end());return res;
}2.2约数个数和约数之和

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
2.3欧几里得算法
辗转相除法计算两个整数的最大公约数GCD
int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}
和最小公倍数LCM之间的关系
GCD(a,b)*LCM(a,b)=a*b
三、欧拉函数
四、快速幂
原始版
#include<bits/stdc++.h>
using namespace std; long long quick_pow(long long a,long long b){//计算a^b次方long long res = 1;//用res保存答案//当b变成0后就可以停止循环了while(b){if(b & 1) res*=a;//如果b当前二进制为1就要乘上这个数b>>=1; //将b末尾的二进制数删掉a*=a; // 将a乘以自己进行翻倍(平方) //比如,开始a==5,接下来a = 5^2,a=5^4,a=5^8,a=5^16....//通过遍历每个在范围内的2的次方数来更新a}return res;
}
int main()
{long long a,b;cin>>a>>b;cout<<quick_pow(a,b);
}快速地求出a^k mol p的结果
前置知识 (a *b *c *d )%p = (((a *b)%p *c)%p *d)%p
即每次乘以下个数前可以先取模,这样最后答案不变
答案不变真的好抽象、
LL quick_pow(LL a, LL b, LL p){ //LL是long long 的缩写//p是要对取模的数字LL ans = 1;while(b){if(b & 1)ans =(ans*a)%p;b >>= 1;a = (a*a) % p;}return ans;}
Example:快速幂求逆元
同余
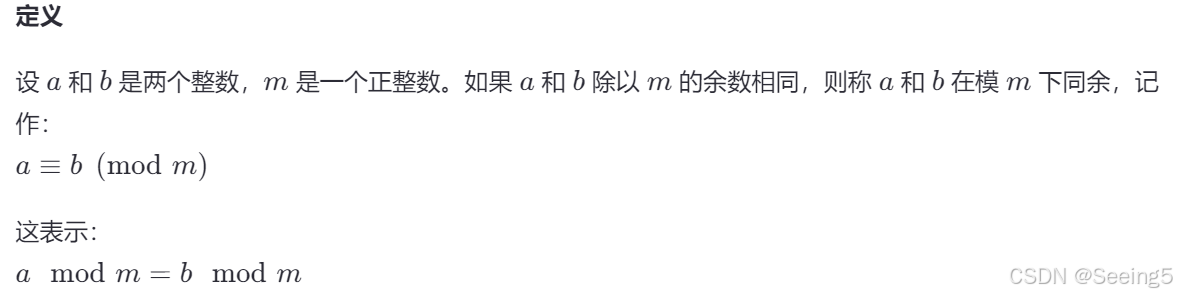
乘法逆元定义

 acwing版本:
acwing版本:

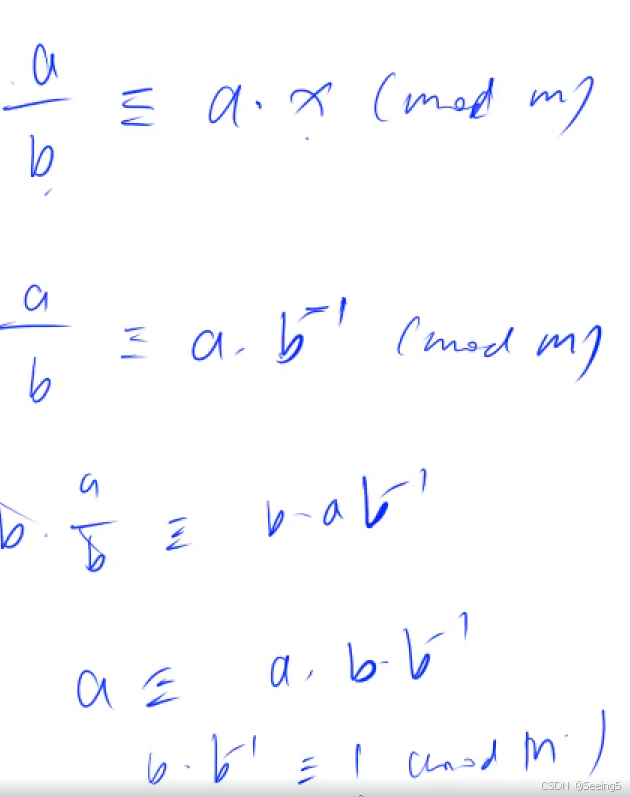
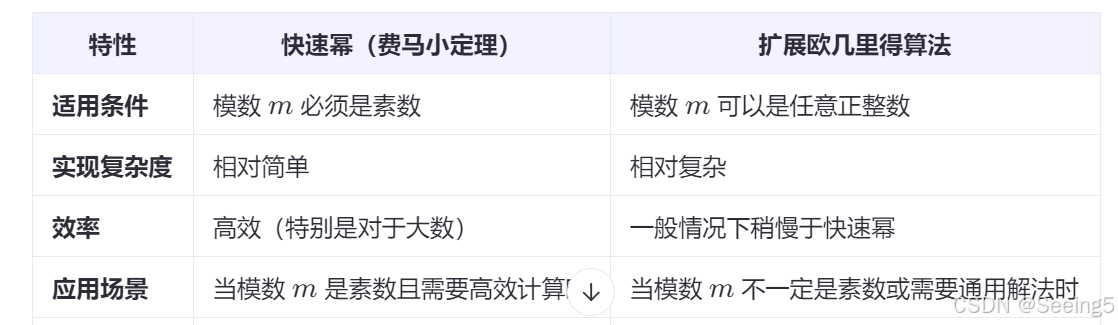
五、扩展欧几里得算法

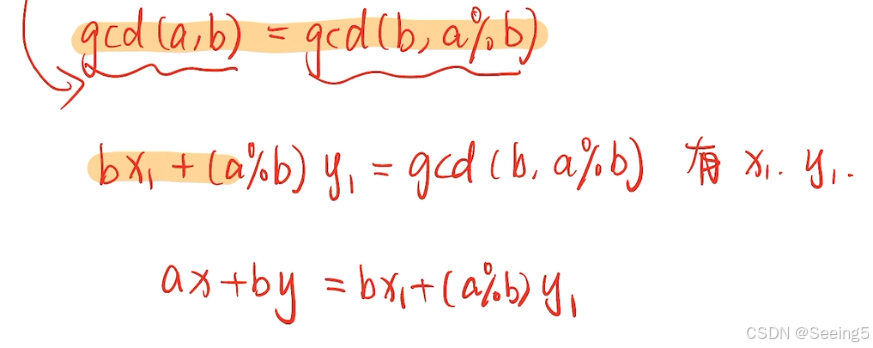
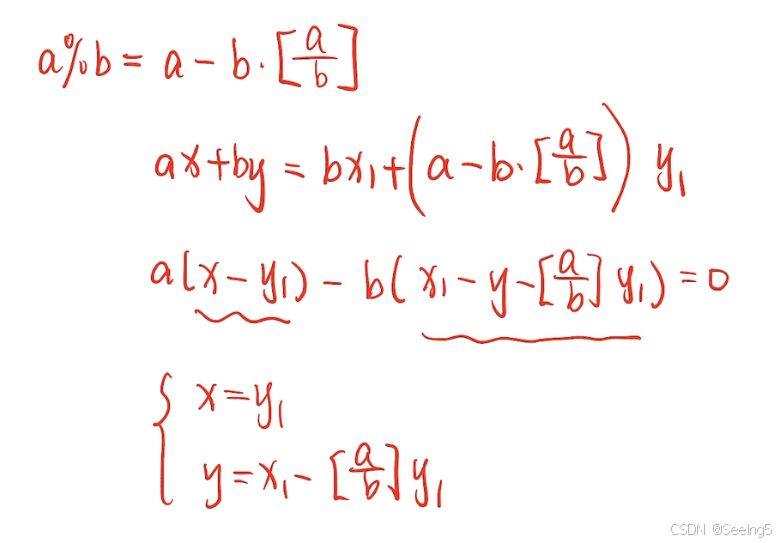

exgcd这个函数里面x和y这两个参数是传引用(pass by reference)进来的,事实上这两个参数也是函数的输出值。根据我们前面推导的式子,每次更新我们想要让 x = y1, 然后 y = x1 - 【a / b】 * y1,所以在调用递归的时候,我们直接把x传成y,然后y传成x,这样下来就相当于x = y1, y = x1,之后我们只需要再把 y -= 【a / b】 * y1 就可以了
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{if (!b){x = 1; y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= (a/b) * x;return d;
}x,y系数的所有解

Example1
 Example2
Example2
// 计算 a 在模 m 下的乘法逆元
int mod_inverse(int a, int m) {int x, y;int gcd = exgcd(a, m, x, y);if (gcd != 1)//a与m不互质,逆元不存在 return -1; else {// x 可能为负数,需要转换为正数int result = (x % m + m) % m;return result;}
}

Example3



取模运算原因