目录
1 简介
2 前序遍历
2.1 问题描述
2.1.1 示例1
2.2 解题思路
2.3 代码实现
3 中序遍历
3.1 问题描述
3.1.1 示例1
3.1.2 示例2
3.1.3 示例3
3.1.4 示例4
3.2 解题思路
3.3 代码实现
4 后序遍历
4.1 问题描述
4.1.1 示例1
4.1.2 示例2
4.2 解题思路
4.3 代码实现
5 总结
1 简介
本文通过代码示例介绍了二叉树的三种深度优先遍历方法——前序遍历(根-左-右)、中序遍历(左-根-右)和后序遍历(左-右-根),并使用递归方式实现。递归方法直观易懂,符合树的天然递归结构,每种遍历方式都遵循固定的访问顺序:前序遍历先访问根节点,再遍历左子树和右子树;中序遍历先遍历左子树,再访问根节点,最后遍历右子树;后序遍历则先遍历左右子树,最后访问根节点。本文提供清晰的 C++ 代码示例,并分析递归的工作原理,帮助读者深入理解二叉树的遍历过程及其应用。
2 前序遍历
2.1 问题描述
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
数据范围:二叉树的节点数量满足 1≤n≤100 1≤n≤100 ,二叉树节点的值满足 1≤val≤100 1≤val≤100 ,树的各节点的值各不相同
示例 1:
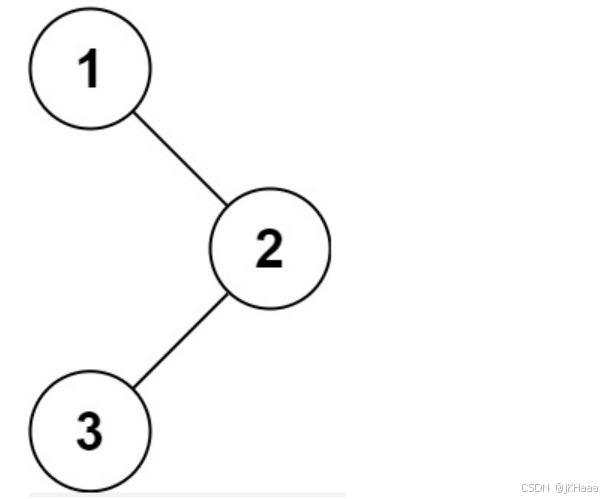
2.1.1 示例1
输入:
{1,#,2,3}
返回值:
[1,2,3]
2.2 解题思路
采用递归方式实现二叉树的前序遍历(根-左-右),并将遍历结果存储在 vector<int> 中。preorderTraversal 函数调用 preorder 递归函数,preorder 依次执行:访问当前节点(存入 result)→ 遍历左子树 → 遍历右子树。递归终止条件是当前节点为空(即 nullptr),此时直接返回。
2.3 代码实现
vector<int> preorderTraversal(TreeNode* root) {// write code herevector<int> result;preorder(root, result);return result;}void preorder(TreeNode* node, vector<int>& result){if(node == nullptr) return;result.push_back(node->val);preorder(node->left, result);preorder(node->right, result);}3 中序遍历
3.1 问题描述
给定一个二叉树的根节点root,返回它的中序遍历结果。
数据范围:树上节点数满足 0≤n≤10000≤n≤1000,树上每个节点的值满足 −1000≤val≤1000−1000≤val≤1000
进阶:空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
3.1.1 示例1
输入:
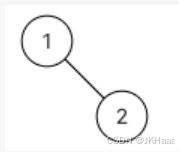
{1,2,#,#,3}
返回值:[2,3,1]
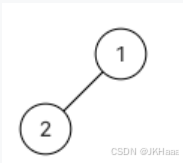
3.1.2 示例2
输入:
{}
返回值:[]
3.1.3 示例3
输入:
{1,2}
返回值:[2,1]
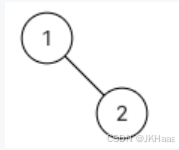
3.1.4 示例4
输入:
{1,#,2}
返回值:[1,2]
3.2 解题思路
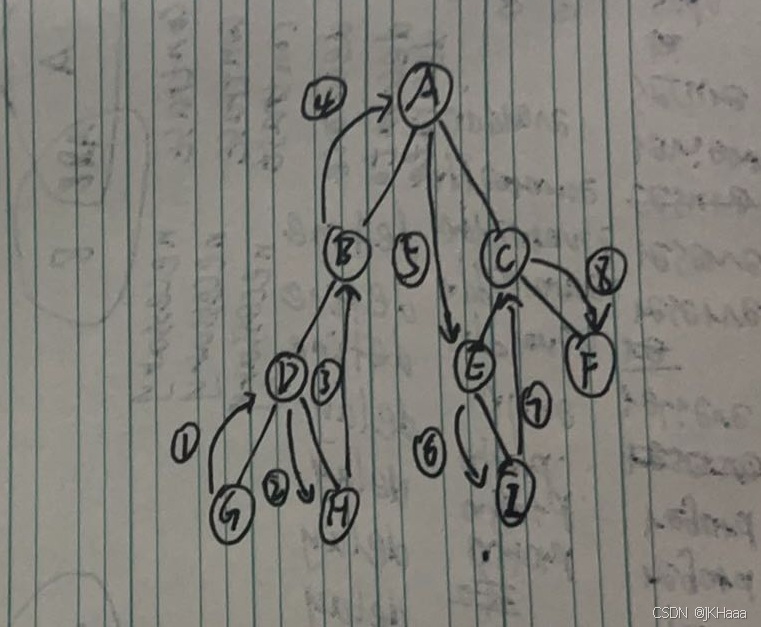
采用递归方式实现二叉树的中序遍历(左-根-右),并将遍历结果存储在 vector<int> 中。inorderTraversal 函数调用 inorder 递归函数,inorder 依次执行:先递归遍历左子树 → 访问当前节点(存入 result)→ 递归遍历右子树。递归终止条件是当前节点为空(即 nullptr),此时直接返回。
3.3 代码实现
vector<int> inorderTraversal(TreeNode* root) {// write code herevector<int> result;inorder(root, result);return result;}void inorder(TreeNode* node, vector<int>& result){if(node == nullptr) return;inorder(node->left, result);result.push_back(node->val);inorder(node->right, result);}4 后序遍历
4.1 问题描述
给定一个二叉树,返回他的后序遍历的序列。
后序遍历是值按照 左节点->右节点->根节点 的顺序的遍历。
数据范围:二叉树的节点数量满足 1≤n≤100 1≤n≤100 ,二叉树节点的值满足 1≤val≤100 1≤val≤100 ,树的各节点的值各不相同
样例图
4.1.1 示例1
输入:
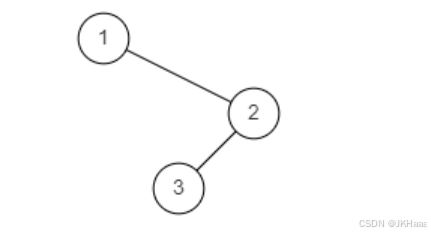
{1,#,2,3}
返回值:
[3,2,1]
4.1.2 示例2
输入:
{1}
返回值:
[1]
4.2 解题思路
采用递归方式实现二叉树的后序遍历(左-右-根),并将遍历结果存储在 vector<int> 中。postorderTraversal 函数调用 postorder 递归函数,postorder 依次执行:先递归遍历左子树 → 递归遍历右子树 → 访问当前节点(存入 result)。递归终止条件是当前节点为空(即 nullptr),此时直接返回。
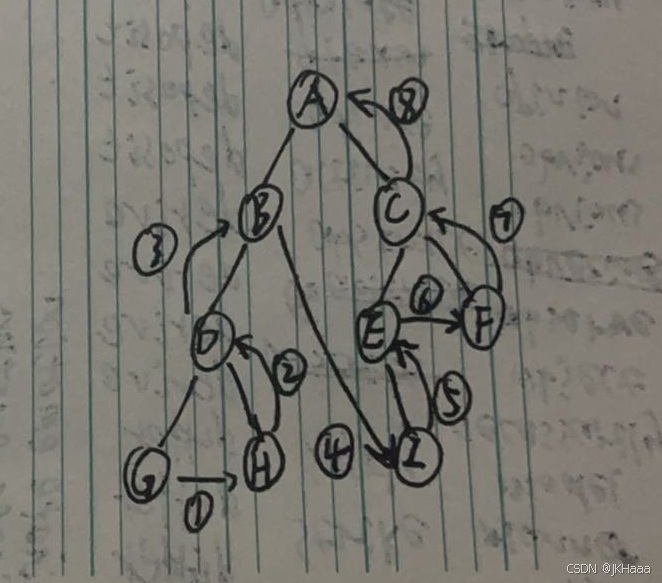
4.3 代码实现
vector<int> postorderTraversal(TreeNode* root) {// write code herevector<int> result;postorder(root, result);return result;}void postorder(TreeNode* node, vector<int>& result){if(node == nullptr) return;postorder(node->left, result);postorder(node->right, result);result.push_back(node->val);}5 总结
本文介绍了二叉树的**前序遍历(根-左-右)、中序遍历(左-根-右)和后序遍历(左-右-根)**三种深度优先遍历方法,并使用递归方式分别实现。递归方法利用二叉树的天然递归结构,使代码简洁直观,每种遍历方式都遵循固定的访问顺序。文章通过示例输入输出、解题思路解析和代码实现,帮助读者掌握不同遍历方法的应用。递归终止条件为当前节点为空(nullptr),以确保遍历完整执行。理解这三种遍历方式对于深入学习树结构及其算法至关重要,能够为后续的二叉树问题提供坚实基础。
