最好看的2018中文在线观看_简历模板大学生_广州seo报价_电子商务

快速幂算法

对于快速幂算法，我们并不是直接暴力进行求解，而是通过快速幂算法，这样算法的时间复杂性由$o(n^2)变为 $o(log|n|)$

50.Pow(x,n)

50.Pow(x,n)

class Solution:def myPow(self, x: float, n: int) -> float:# 首先判断这个n是否小于0if n < 0:n = -nx = 1 / x#  ans 是存储结果ans  = 1while n != 0:if n&1 ==1:ans*= x# 每次的x 都需要乘xx*= xn=n>>1return ans

2961.双模幂运算

2961.双模幂运算

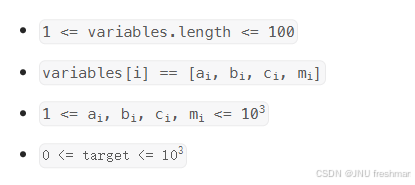
思路分析：由于涉及的幂次很大，所以不可能一一求解，所以使用快速幂算法，python 内置的pow函数就可以使用快速幂算法

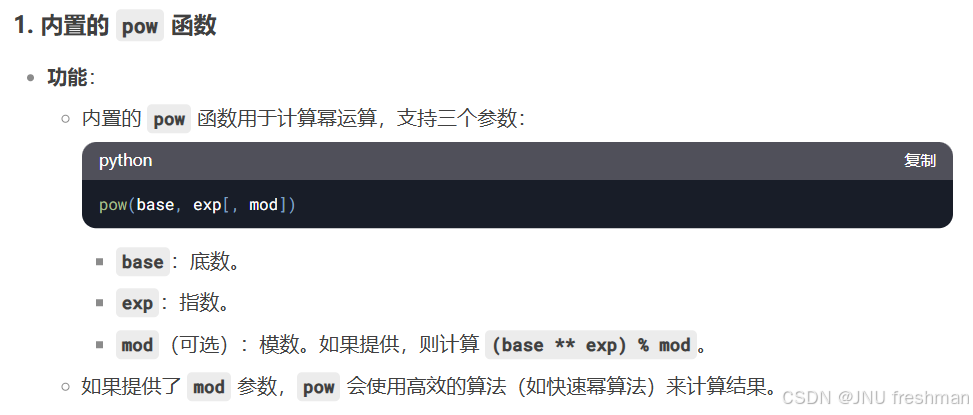
class Solution:def getGoodIndices(self, variables: List[List[int]], target: int) -> List[int]:# 可以看到幂次很大，所以考虑使用快速幂进行求解# python 有内置的函数pow(a,b,m) 用于求解 a^b mod mans = []for i ,c in enumerate(variables):if pow(pow(c[0],c[1],10),c[2],c[3]) == target:ans.append(i)return ans

费马小定理

欧拉定理

任何一个数都可以表示为质数的乘积

取模

对于取模的运算，建议先看看灵神的总结

模运算的世界：当加减乘除遇上取模（模运算恒等式/费马小定理/组合数）

取模的情况

加减乘除的情况

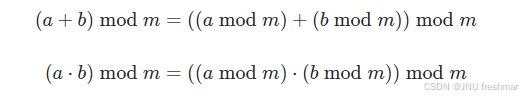
负数这边的情况使用到了欧拉定理

3379.转换数组

思路分析：就是通过正常的计算即可，因为对于python 来说，负数取模并不用转化，它计算的时候直接会得到非负数的结果

class Solution:def constructTransformedArray(self, nums: List[int]) -> List[int]:# 取模的意义在于循环n = len(nums)result = [0]*n for i in range(n):if nums[i] == 0:result[i] = nums[i]if nums[i]<0:j = (i-abs(nums[i]))%n result[i] = nums[j]if nums[i]>0:j = (i+nums[i])%n result[i] = nums[j]return result