Set集合
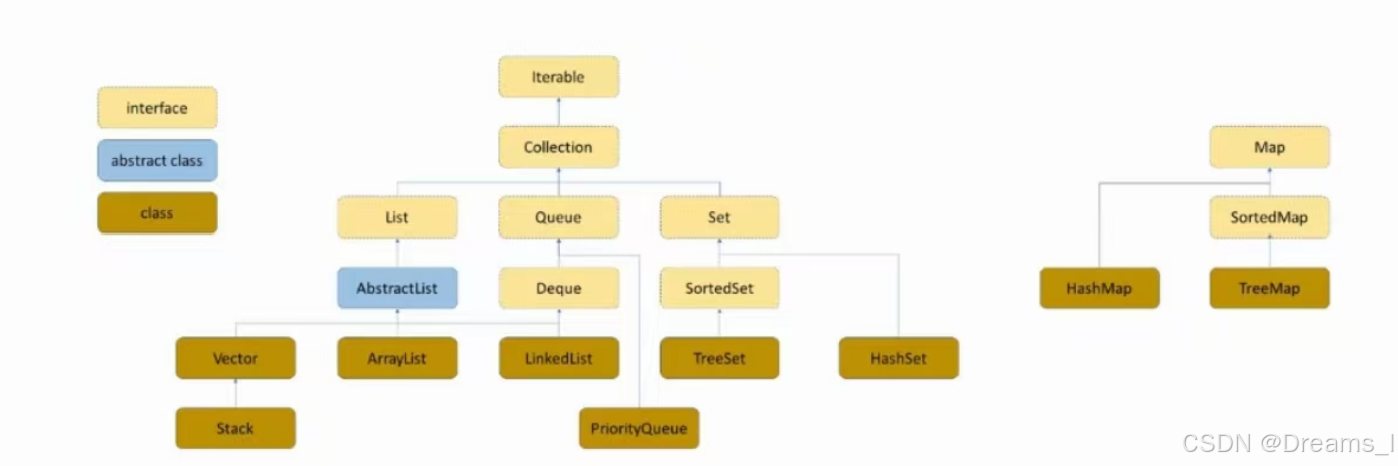
Set的核心特点：
Set继承了Collection。
保存的元素不会重复。
保存的元素不能修改。
保存的元素无序，和List不同，如果有两个：List {1，2，3}，List {2，1，3}，认为两个List不相同，但是将List换成Set，则认为两个Set相同。
Set的核心操作：add，remove，contains。
JAVA标准库中的Set：
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
import java.util.TreeSet;public class myset {public static void main(String[] args) {Set<String> set = new TreeSet<>();Set<String> set2 = new HashSet<>();set.add("aaa");set.add("bbb");set.add("ccc");set.add("vvv");set.add("dww");System.out.println(set);//判断Set是否为空System.out.println(set.isEmpty());//foreach 遍历Setfor (String i: set) {System.out.println(i);}//Iterator接口(迭代器)遍历Iterator<String> d = set.iterator();while (d.hasNext()){System.out.println(d.next());}}
}Set是接口，需要创建实现Set的类，可以通过两种方式进行实现，TreeSet和HashSet，TreeSet的底层是红黑树，Hashset底层是哈希表这种数据结构。
Map
Map可以想象成Set的进一步，和Set非常相似，Set上保存的只是"key",而Map上保存的是键值对"key-value"，对于Set来说，key是唯一的，而对于Map，Key是唯一的，而value不唯一。
同样的Map也需要实现类，这里提供了TreeMap和HashMap。
Map的核心操作：
get，put，remove。
import java.util.*;public class map {public static void main(String[] args) {Map<String, String> map = new TreeMap<>();map.put("及时雨", "宋江");map.put("小李广", "花容");map.put("呼宝义", "宋江");map.put("黑旋风", "李逵");System.out.println(map.get("及时雨"));System.out.println(map.get("玉麒麟"));// //获取键值对的个数System.out.println(map.size());
//
// //设置默认值System.out.println(map.getOrDefault("yuqiling","saasas"));System.out.println(map.getOrDefault("及时雨","sds"));// //判定key是否存在System.out.println(map.containsKey("kkk"));
//
// //判定values是否存在System.out.println(map.containsValue("李逵"));
//
// //拿到所有key，存一个set中Set<String> i = map.keySet();System.out.println(i);// //拿到所有valuesCollection<String> a = map.values();System.out.println(a);//遍历Map所有键值对,是一个很大的开销操作，需要慎用，Map的初心是解决key-values的映射关系，不是遍历//entry--条目for(Map.Entry<String,String>entry : map.entrySet()){System.out.println(entry.getKey()+" "+entry.getValue());}System.out.println(map.isEmpty());map.clear();}
}二叉搜索树
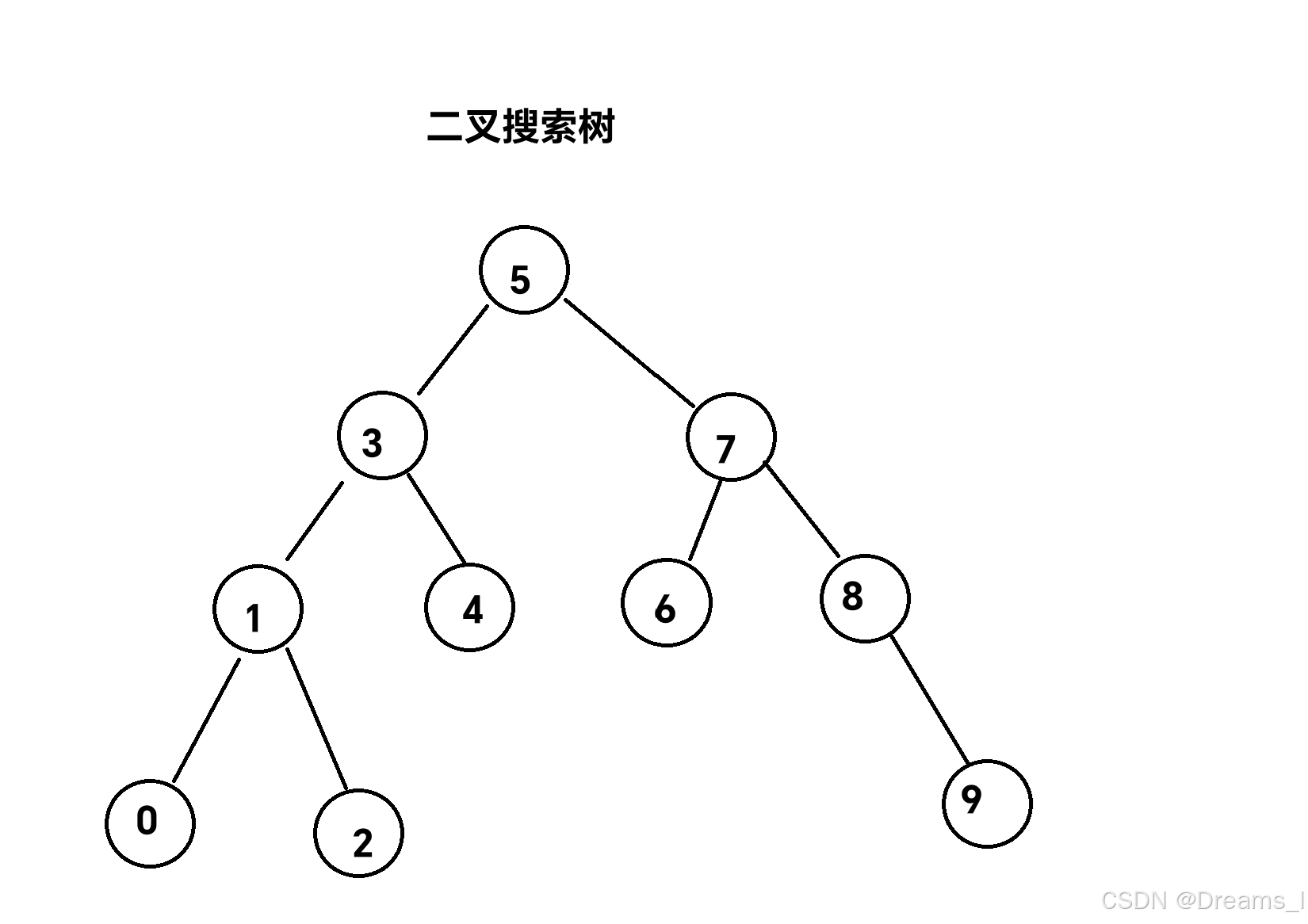
前面的TreeMap和TreeSet中tree是二叉搜索树，二叉搜索树的特点是根节点要小于左节点，大于右节点，它的左右子树都是二叉搜索树。
二叉搜索树的目的是为了高效查找，对于红黑树这种平衡的二叉树搜索树，时间复杂度是Olog（n）。
模拟实现二叉搜索树
1.添加新元素：先判断是否为空树，如果为空，就让root = newnode；不为空，就在树中寻找合适的位置进行插入，同时记录curparent的位置，最后判断要插入值和curparent的大小，如果大于curparent，就插左边，反之插右边。
2.找元素在不在表中：先判断是否为空树，如果是，返回null，不是就遍历二叉搜索树，找到返回值，反之null。
3.删除元素：先找到要删除的元素，判断要删除元素cur的子树情况：
3.1 cur的左右子树都为空。
3.2 cur 的左为空，右不为空。
3.3 cur的左不为空，右为空。
3.4 cur的左右子树都不为空：找到cur右子树的最左边的叶子节点，将cur和它进行交换，然后将其删除。
class Node{public int key;public Node right = null;public Node left = null;public Node(int key) {this.key = key;}
}
public class BinarysearchTree {private Node root = null;public void insert(int key){Node newnode = new Node(key);if(root==null){root = newnode;return;}Node cur = root;Node curparent = null;while(cur!=null){if(cur.key>key){//向左找curparent = cur;cur = cur.left;} else if (cur.key<key) {curparent = cur;cur = cur.right;}else{return;}}if(curparent.key>key){curparent.left = newnode;}else{curparent.right = newnode;}}public Node find(int key){if(root == null){return null;}Node cur = root;while (cur!=null) {if(cur.key>key){cur = cur.left;} else if (cur.key<key) {cur = cur.right;}else{return cur;}}return null;}public void removenode(int key){if(root==null){return ;}Node cur = root;Node curparent = null;while(cur!=null){if(cur.key>key){curparent = cur;cur = cur.left;} else if (cur.key<key) {curparent = cur;cur = cur.right;}else{remove(curparent,cur);return;}}}public void remove(Node parent,Node cur){//cur没有子树if(cur.left==null&&cur.right==null){if(cur==root){root = null;return;}if(cur==parent.right){parent.right = null;return;}if(cur==parent.left){parent.left = null;return;}return;}//cur只有左子树if(cur.left!=null&&cur.right==null){if(cur==root){root = cur.left;return;}if (cur==parent.left){parent.left = cur.left;return;}if(cur==parent.right){parent.right = cur.left;return;}return;}//cur只有右子树if(cur.right!=null&&cur.left==null){if(cur==root){root = cur.right;return;}if(cur == parent.right){parent.right = cur.right;return;}if(cur==parent.left){parent.left = cur.right;return;}return;}//cur有左右子树if(cur.left!=null&&cur.right!=null){Node goat = cur.right;Node goatparent = null;while(goat.left!=null){goatparent = goat;goat = goat.left;}cur.key = goat.key;if(goat==goatparent.left){goatparent.left = goat.right;}else{goatparent.right = goat.right;}}}//打映操作public void inoder(Node root){if(root==null){return ;}inoder(root.left);System.out.println(root.key);inoder(root.right);}public void print(){inoder(root);}public static void main(String[] args) {int[] arr = {1,3,2,6,5,7,8,9,10,0};BinarysearchTree in = new BinarysearchTree();for (int i: arr) {in.insert(i);}in.print();}}这里删除操作的关于将交换的元素删除时，不能简单的将goatparent.left = goat.right，而是要判断goat的指向
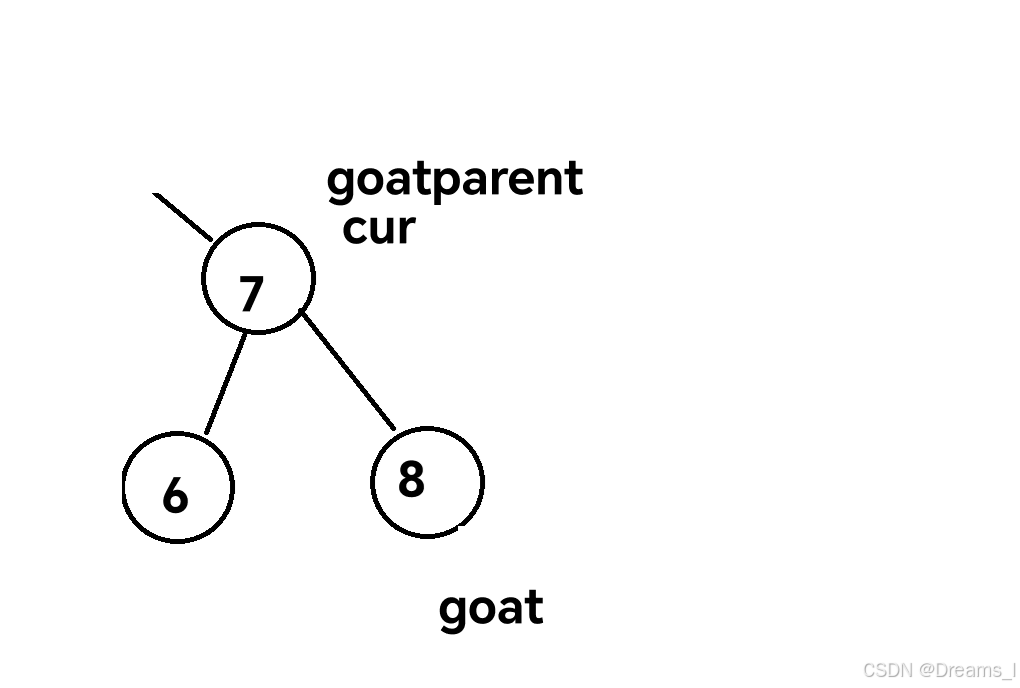如果是上面的情况就要goatparent.right = goar.right。
哈希表
哈希表这种数据结构，也是为了高效查找，查找的时间复杂度是O（1），删除的时间复杂度也是O（1）。
通过一个场景理解哈希表：
给定一个任意长度的数组，约定数组里的元素范围是0-99，要统计每个数字出现的次数。
我们可以申请一个长度100的数组，将元素作为新数组的下标，元素出现一次就让新数组对应元素加一，最后遍历数组，统计出现一次的元素。
那么如果要存储的元素是小数，字符或字符串呢？又要如何约定新数组的范围呢，这时我们可以约定一个数组，通过一个哈希函数将元素进行转换，来映射到合法的数组下标上。
但是如果元素的数量大于数组的空间，就会有重复的情况，这种现象叫哈希冲突。
解决哈希冲突的方法叫开散列(哈希桶)，通过链表的方式将重复的元素链接，这样在寻找时通过哈希值找到相应下标，然后在遍历链表，进行查找或删除，就能快速找到。
这里的遍历链表操作时间复杂度还是O（1），我们可以设置一些手段，限制链表的长度（虽然是链表，但长度非常短），限制列表的手段是负载因子 = 整个哈希表保存的元素个数/数组的长度（相当链表的平均长度），实际操作中可以根据负载因子设定阈值，随着哈希表的元素增加，负载因子增加，达到阈值就会触发扩容操作。
哈希表特点：
本质上是一个通过利用了数组下标操作比较高效特点实现的一个数据结构。
通过哈希函数把要保存的内容映射到数组下标上。
如果出现冲突，在通过开散列的方式，解决冲突。
引入负载因子，限制链表的长度，保证最终的复杂度仍然是O(1)级别（当链表超过一定长度，就会自动转变成红黑树）。
哈希函数：
哈希函数是将元素映射到哈希表上的重要方法。
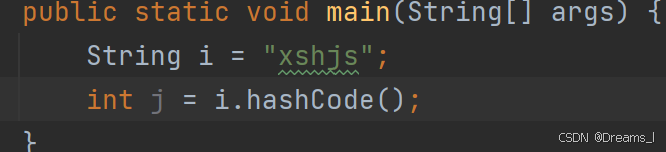
在JAVA中类Object提供了一个hashCode方法，其他类自然继承了这个类，不同的类有不同的方式重写这个类。
实现哈希表：
1.增加键值对：首先要将key通过哈希函数得到哈希值，寻找到数组中对应的下标，开始遍历链表；如果这个值在表中，若是HashMap，则直接返回，若是HashTree,则将值修改；如果不在表中，就进行头插。
2.根据key寻找value：先根据key得到哈希值，再根据哈希值得到对应的数组下标，开始遍历。
3.删除键值对：
3.1.链表为空：直接返回空。
3.2.头节点是要寻找的key：让头节点等于下一个节点。
3.3.一般情况：记录要删除元素和其上一个值，进行删除。
public class HashTable {static class Node{public int key ;public int value;public Node next;public Node(int key, int value) {this.key = key;this.value = value;}}public Node[] table = new Node[1000];public int size = 0;public int hashCode(int key){return key%table.length;}//插入键值对public void insert(int key,int value){int index = hashCode(key);Node head = table[index];//先遍历链表，看是否有这个键，如果有就将其value更新for(Node cur = head;cur!=null;cur = cur.next){if(cur.key == key){cur.value = value;return;}}//没有就将新节点以头插的方式插入Node newnode = new Node(key,value);newnode.next = head;table[index] = newnode;size++;//扩容if((double)size/ table.length>0.75){resize();}}public void resize(){Node[] newtable = new Node[table.length*2];for (int i = 0; i < table.length; i++) {for (Node cur = table[i]; cur!=null ; cur = cur.next) {Node newcode = new Node(cur.key,cur.value);int index = cur.key% newtable.length;newcode.next = newtable[index];newtable[index]= newcode;}}table = newtable;}//根据键获取值public Integer get(int key){int index = hashCode(key);Node head = table[index];for (Node cur = head;cur!=null;cur=cur.next){if(cur.key==key){return cur.value;}}return null;}//删除键值对public void remove(int key){int index = hashCode(key);//判断是否为空链表if(table[index]==null){return;}//判断头节点是否为要删除元素if(table[index].key== key){table[index] = table[index].next;size--;return;}//一般情况Node prv = table[index];Node cur = table[index].next;for (;cur!=null;cur=cur.next){if(cur.key==key){prv.next = cur.next;size--;return;}prv = cur;}}