写卷子前准备:二进制串、卡诺图的数序、分析与设计的步骤,直接写上省的忘了
进制转化
二进制
刚开始做题前可以把0-9次方的列出来

十进制转二进制:不断除以2得到余数,直到商为0,再将余数倒着拼起来即可。
如十六进制,则可以把二进制串化成四位取一位十六进制,
八进制,把二进制串化成三位取一位八进制数
小数部分(二进制与十进制对应):0.1-0.5 , 0.01-0.25 , 0.001-0.125
每次*2,有1取1,不够1则0,与整数不同,要从上往下取,转化为二进制

二进制的小数部分,转化为十进制,按照对应位次,*2的次方

八进制 十六进制同理
八进制转化为十进制,(与二进制同理,倒着取余数)
小数部分同理,乘以对应的进制,整数部分倒是可以二进制串划分直接转换

原、反、补码
原码:0正1负,符号位加二进制数的绝对值构成,
反码:正数与原码相同,负数:除符号位,其他按位取反(相反数)
补码:正数与原码相同,负数:除符号位,其他按位取反(相反数),再在最低位加1
十进制编码也称为BCD码,其本质是十进制,表现形式为二进制代码
每一位十进制,转化为四位二进制代码串
逻辑代数
常见规则

后面两个 可以直接忽略后面多余串
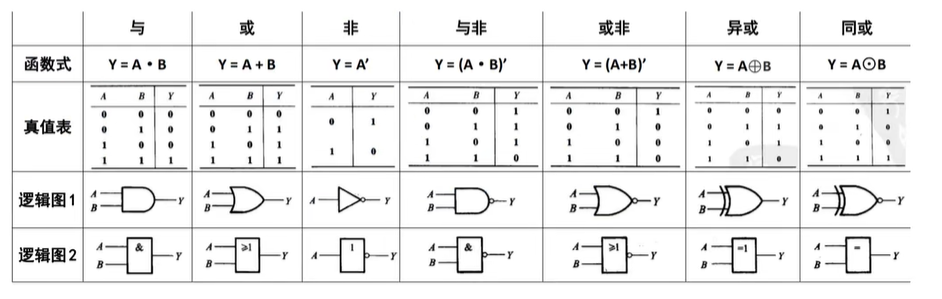
逻辑图表达式
与 是 半圆 ,或 是尖一点的,且的符号
有。则为非
最大/小项
最小项 用mi表示,1表示原变量,i为二进制转为十进制的值
最大项 用Mi表示,0表示原变量
可以直接根据表达式来直接写出最小项之和,

逻辑函数的化简

卡诺图化简
对角不相邻(例如左上、右下),不能连


卡诺图圈中 元素取值变化的不取,剩下的写出表达式加起来即可

无关项化简
约束条件就是无关项,把无关项画×就行,

例题

四个角的可以四个互连

给真值表的
找出其中的1,填进卡诺图,化简即可

根据电路写出逻辑表达式
记住逻辑电路表达式符号即可
化为最小项之和

组合逻辑电路-只与当前输入有关
时序逻辑电路-当前输入,电路状态(之前输入)
组合逻辑电路分析与设计
分析
确定有几个输入几个输出,写输出变量表达式--化简输出表达式(卡诺图)--列真值表。功能分析
电路图-真值表
表达式-化简-真值表-功能分析


化简时的反演定律-拆开变对方
设计
确定输入输出变量(写出来)、
先根据要求画出真值表-得出表达式-化简(利用卡诺图)-画电路图
看清题目要求,与非门、与或门
或者可以直接根据真值表化简-得到表达式


设计题例

化为与非--最好两次取反--摩根定理
编码器
时序电路分析与设计
分析
写方程-列状态-说功能

确定电路类型、同步/异步--输出时钟方程-次态方程--真值表(状态表)-状态转移表(现态、次态、输出)--状态图(/Z)--检查能否自启动(在无效状态下是否能回到有效状态(不存在无效状态的循环))--画时序图(直接根据状态转移图)、描述功能。
可以没有组合电路,不能没有触发器

分类


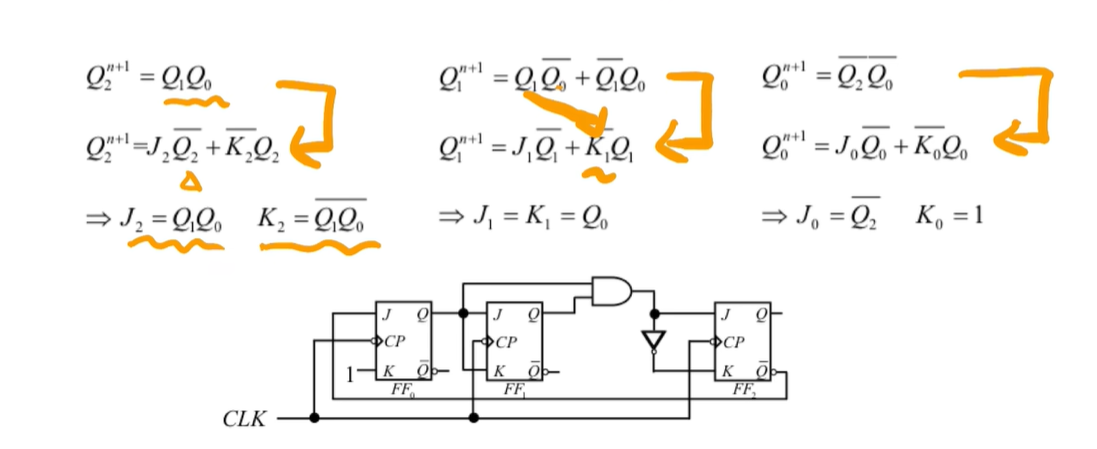
驱动方程(触发器的属性)和状态方程转化:驱动方程(触发器相关属性)代入特性方程(Qn+1),得到次态方程(状态方程)
驱动方程(激励方程):直接看逻辑电路图,读出来触发器的表达式

例题1
.状态转移图--找当前次态对应的下一个现态,的次态为下一个转移的装填
根据状态转移表画波形图

例题2

读激励方程,看清怎么连的,是否连在了一起


可以在旁边写出触发器排列,简单明了

设计
根据要求--状态图--真值表--状态方程(卡诺图化简得到次态方程)--激励方程(JK)--输入输出时钟方程-逻辑电路图(带触发器)
Mealy型-当前状态、输入
moore型-只与状态有关

例题
状态图的顺序要和状态表对应,别搞反了。如都是Q3Q2Q1,图和表就都是
状态图没涉及的现态对应的次态都可以设置为无关状态,便于卡诺图化简,无关项用于辅助,不一定非得画进去


同步型,所以CLK(CP)连到一起

记住触发器的图案怎么画
例题2

真值表到卡诺图化简,多项的不必特意反过来
得到次态方程以后,还要把无效状态填进去,得到新的转移图,即拥有自启动的功能


触发器


波形图:在有效脉冲下维持之前的状态不变

空翻:1个时间段内变换2次

边沿触发器
只在脉冲边缘处发生改变
JK触发器:00不变,01置0,10置1,11翻转

上升沿、下降沿有效判断:有。的是下降沿,无圈就是上升沿

画波形图



