目录
- 前言
- 非递减子序列
- 全排列
- 全排列II
- 总结
前言
今天是学习回溯算法的第四天,我们继续来一起学习回溯算法蕴含的逻辑处理,希望博主记录的内容能够对大家有所帮助 ,一起加油吧朋友们!💪💪💪
非递减子序列
LeetCode题目链接
这道题就是给一个整数数组,然后要返回数组里所有不同的递增子序列,要体现递增,子序列长度大于1

我们来思路梳理
- 递归遍历数组中的每个元素,构建所有可能的递增子序列🤔 在每层递归中使用一个集合(或类似结构)来记录已经选择过的数字,避免在同一层中重复选择相同的数字🤔在递归时,确保每次选择的元素大于或等于当前序列的最后一个元素,以保证子序列是递增的🤔 当递增子序列的长度达到两位或以上时,将其加入结果集
我们进一步来梳理回溯三要素
- 确定递归函数的参数和返回值
//nums: 输入的整数数组
//startIndex: 当前递归处理到的数组起始位置
//path: 当前递增子序列(构建中的路径)
//result: 存储所有不同的递增子序列的列表
//used: 用于记录在当前递归层是否已经使用过某个数字,防止同层次中重复选择相同的元素
//递归函数不需要返回值,结果会直接存入 result 列表中
private void backtracking(int[] nums, int startIndex, List<Integer> path){}
- 回溯终止条件( 每次递归进入新层时,如果构建中的路径
path长度至少为 2,说明找到了一个合法的递增子序列,将其加入结果集🤔)
if(path.size() >= 2){result.add(new ArrayList<>(path));
}
- 单层搜索过程( 使用
startIndex开始遍历数组,从当前索引位置向后遍历, 逐一判断当前元素是否可以加入当前子序列(即该元素是否大于或等于path中的最后一个元素), 使用Set或类似的结构避免在同一层中重复选择相同的元素,防止生成重复的子序列, 加入元素后递归,回溯时移除当前元素以便继续尝试其他组合🤔)
Set<Integer> used = new HashSet<>(); //记录当前层已经使用过的元素来去重for(int i = startIndex; i < nums.length; i++){ //单层搜索过程if(used.contains(nums[i])){//去重continue;//跳过}if(!path.isEmpty() && nums[i] < path.getLast()){//判断递增continue;}path.add(nums[i]);used.add(nums[i]);//记录元素防止本层重复使用backtracking(nums, i + 1, path);//递归进入下一层path.removeLast();//回溯
}
完整的回溯代码如下
class Solution { List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtracking(nums, 0, new ArrayList<>());return result;}private void backtracking(int[] nums, int startIndex, List<Integer> path){if(path.size() >= 2){//终止条件result.add(new ArrayList<>(path));}Set<Integer> used = new HashSet<>(); //记录当前层已经使用过的元素来去重for(int i = startIndex; i < nums.length; i++){ //单层搜索过程if(used.contains(nums[i])){//去重continue;//跳过}if(!path.isEmpty() && nums[i] < path.getLast()){//判断递增continue;}path.add(nums[i]);used.add(nums[i]);//记录元素防止本层重复使用backtracking(nums, i + 1, path);//递归进入下一层path.removeLast();//回溯}}
}
全排列
leetCode题目链接
给定一个没有重复数字的序列,返回其所有可能的全排列🤔
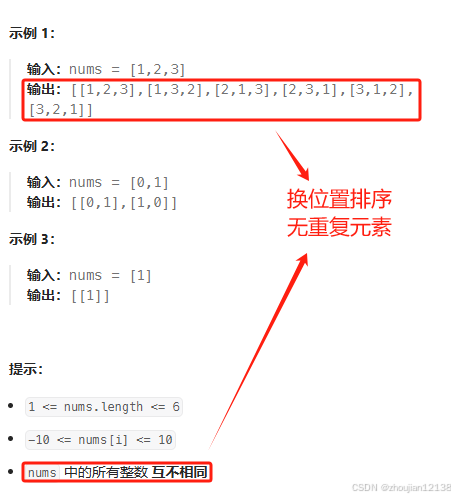
我们来思路梳理
- 通过递归构造所有可能的排列,每次从剩余未使用的数字中选择一个加入当前排列🤔 在递归过程中,将当前数字加入当前路径(即部分排列),并标记该数字已被使用。完成该排列后,回溯时撤销选择,恢复状态以尝试其他可能性🤔 当当前路径的长度等于输入序列的长度时,表示找到一个完整的排列,将其加入结果集🤔 因为输入数字没有重复,不需要考虑去重问题
我们来进一步梳理回溯三要素
- 确定递归函数的参数和返回值
//nums: 输入的整数数组
//used: 一个布尔数组,记录哪些数字已经被使用
//path: 当前排列的路径
//result: 存储所有可能排列的列表
//递归函数不需要返回值,结果会直接存入result列表中
List<List<Integer>> result = new ArrayList<>();
private void backtracking(int[] nums, boolean[] used, List<Integer> path){}
- 回溯终止条件( 当当前路径
path的长度等于输入数组的长度时,表示已经找到一个完整的排列,将其加入结果集中🤔)
if(path.size() == nums.length){result.add(new ArrayList<>(path));return;
}
- 单层搜索过程(遍历数组中的每一个元素,判断它是否已经被使用过。如果没有被使用,则将其加入当前排列路径🤔 递归调用后继续处理剩余未使用的数字🤔 回溯时,撤销当前的选择,标记该元素未被使用,以便继续尝试其他排列组合 )
for(int i = 0; i < nums.length; i++){if(used[i])continue;//如果数字使用过则跳过//选择当前数字加入排列path.add(nums[i]);used[i] = true;backtracking(nums, used, path);//递归继续构造剩余数字的排列//回溯used[i] = false;path.removeLast();
}
完整的回溯代码如下
class Solution {List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> permute(int[] nums) {boolean[] used = new boolean[nums.length];backtracking(nums, used, new ArrayList<>());return result;}private void backtracking(int[] nums, boolean[] used, List<Integer> path){if(path.size() == nums.length){result.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++){if(used[i])continue;//如果数字使用过则跳过//选择当前数字加入排列path.add(nums[i]);used[i] = true;backtracking(nums, used, path);//递归继续构造剩余数字的排列//回溯used[i] = false;path.removeLast();}}
}
全排列II
LeetCode题目链接
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列

我们来进行思路梳理
- 首先对
nums进行排序,这样相同的数字会相邻,便于后续处理重复项🤔 递归生成排列,构造排列时需要判断当前元素是否已经被使用。对于相邻的相同元素,如果上一个相同元素未被使用,当前元素也不应被使用(避免重复排列)🤔 在递归中选择未使用的数字加入当前路径(部分排列),并标记为已使用,回溯时撤销选择🤔 当当前路径的长度等于输入数组的长度时,表示找到一个完整排列,将其加入结果集中🤔
我们来进一步梳理回溯三要素
- 确定递归函数的参数和返回值
//nums: 输入的整数数组(包含重复数字)
//used: 一个布尔数组,记录哪些数字已经被使用
//path: 当前排列的路径
//result: 存储所有不重复排列的列表
//递归函数不需要返回值,结果会直接存入 result 列表中
List<List<Integer>> result = new ArrayList<>();
private void backtracking(int[] nums, boolean[] used, List<Integer> path) {}
- 回溯终止条件( 当当前路径
path的长度等于输入数组的长度时,表示已经找到一个完整的排列,将其加入结果集中🤔)
if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 将当前排列加入结果集return;
}
- 单层搜索过程( 遍历数组中的每一个元素,判断它是否已经被使用过。如果没有被使用,并且当前元素不是和上一个相同且上一个未被使用(避免重复),则将其加入当前排列路径🤔 递归调用后继续处理剩余未使用的数字🤔 回溯时,撤销当前的选择,标记该元素未被使用,以便继续尝试其他排列组合 )
for(int i = 0; i < nums.length; i++){//同一层中如果当前数字和前一个数字相同,且前一个未使用过,则跳过if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;//去重if (used[i])continue; //如果当前数字已经被使用过,跳过该数字path.add(nums[i]);used[i] = true;backtracking(nums, used, path);//回溯used[i] = false;path.remove(path.size() - 1);
}
完整的回溯代码如下
class Solution {List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> permuteUnique(int[] nums) {Arrays.sort(nums);boolean[] used = new boolean[nums.length];backtracking(nums, used, new ArrayList<>());return result;}private void backtracking(int[] nums, boolean[] used, List<Integer> path) {//终止条件if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 将当前排列加入结果集return;}//单层搜索过程for(int i = 0; i < nums.length; i++){//同一层中如果当前数字和前一个数字相同,且前一个未使用过,则跳过if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;//去重if (used[i])continue; //如果当前数字已经被使用过,跳过该数字path.add(nums[i]);used[i] = true;backtracking(nums, used, path);//回溯used[i] = false;path.remove(path.size() - 1);}}
}
总结
今天的回溯就学到这里啦,去重的话又有了不一样的处理方式,但处理逻辑大差不差,大家只需梳理清楚每层递归与回溯即可,奥利给✊✊✊
