1.2 数制
数制:多位数码中的每一位数的构成及低位向高位进位的规则
目标:掌握进制数的转换
1.2.1进制介绍:
1.十进制介绍
十进制采用0, 1, 2, 3, 4, 5, 6, 7, 8, 9十个数码,其进位的规则是“逢十进一”
![]()
各位的权都是10的幂。
2.二进制介绍
二进制数只有0、1两个数码,进位规律是:“逢二进一”
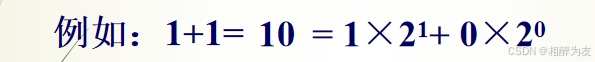
各位权都是2的幂
二进制的优点: ……
二进制数波形表示: 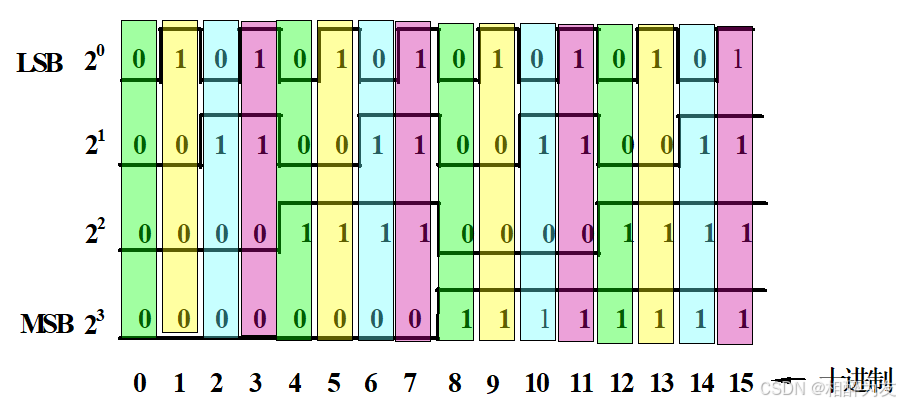
二进制数据的传输:
在时钟脉冲CP控制下,数据由最高位MSB到最低位LSB 逐位送
(1)串行传输
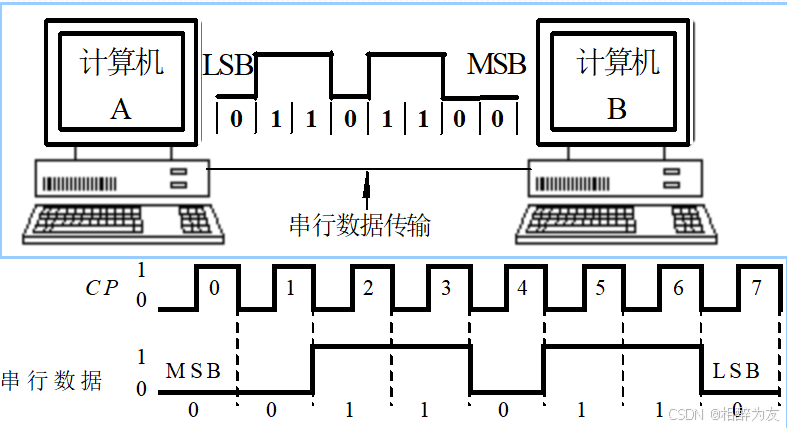
2)并行传输
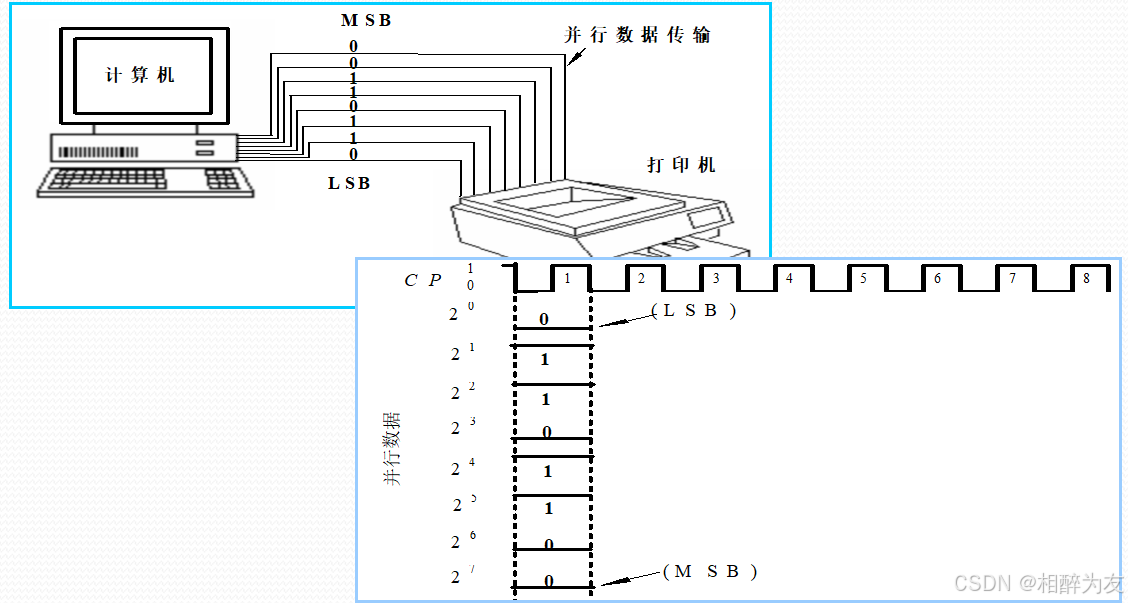
3.十六进制
介绍:
十六进制数中只有0, 1, 2, 3, 4, 5, 6, 7, 8, 9 , A、B、C、D、E、F十六个数码,进位规律是“逢十六进一”。各位的权均为16的幂。
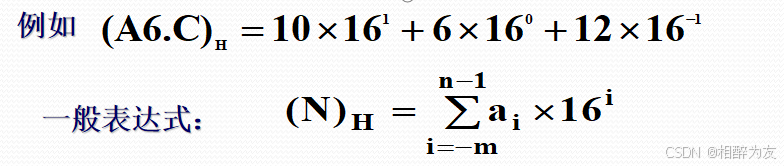
优点:
- 与二进制之间的转换容易;
- 计数容量较其它进制都大(十六进制可计至 (FFFF)H = (65535)D,即64K。其容量最大)
- 书写简洁
4.八进制
八进制数中只有0, 1, 2, 3, 4, 5, 6, 7八个数码,进位规律是“逢八进一”。各位的权都是8的幂。
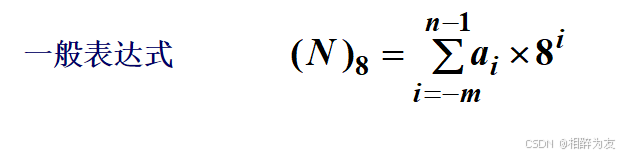
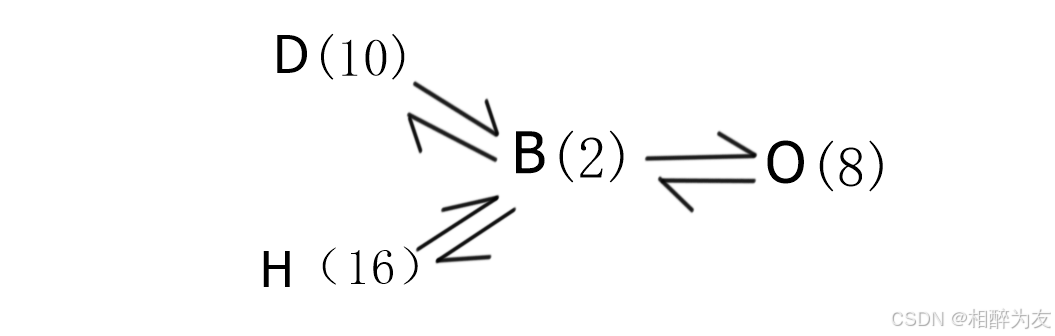
1.2.2进制之间的转换
1.十(D)>>>二(B)的转换
1.整数部分的转换:
“辗转相除”法:
将十进制数连续不断地除以2 , 直至商为零,所得余数由低位到高位排列,即为所求二进制数

位权估算法:

2.小数的转换 :
(1)乘二取整,直至为零:

可见,将十进制小数乘以2,所得乘积的整数即为b-1
所以不难推知,将十进制小数每次摸去上次所得积中的整数再乘以2, 直到满足误差要求进行“四舍五入”为止,就可完成由十进制小数 转换成二进制小数

(2)位权拼凑法:
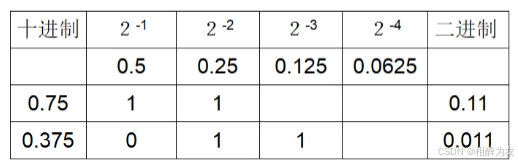
2.N(B|O|H) >>>十(D) 进制的转换
R为位权,N为数值,Ki为位系数
3.二(B)&&十六(H)的进制转换
二进制转换成十六进制:
将每四位二进制数表示一位16进制数,即 0000~1111 表示 0-F
由小数点开始,整数部分高位补零,小数部分低位补零
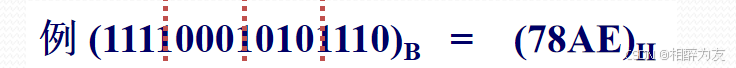
十六进制转换成二进制:
每位16进制数展开成四位二进制数,排列顺序不变即可
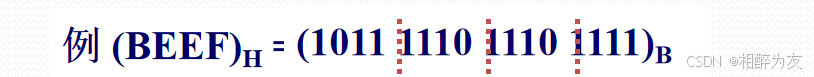
3.二(B)&&八(O)的进制转换
将三位二进制数表示一位八进制数,即 000~111 表示 0~7
由小数点开始,整数部分自右向左,小数部分自左向右,三位一组,不够三位的添零补齐(切记不可忽略低位的0)

1.3 算术运算
1、无符号二进制
加法:逢二进一
减法:缺1高补

乘法
除法
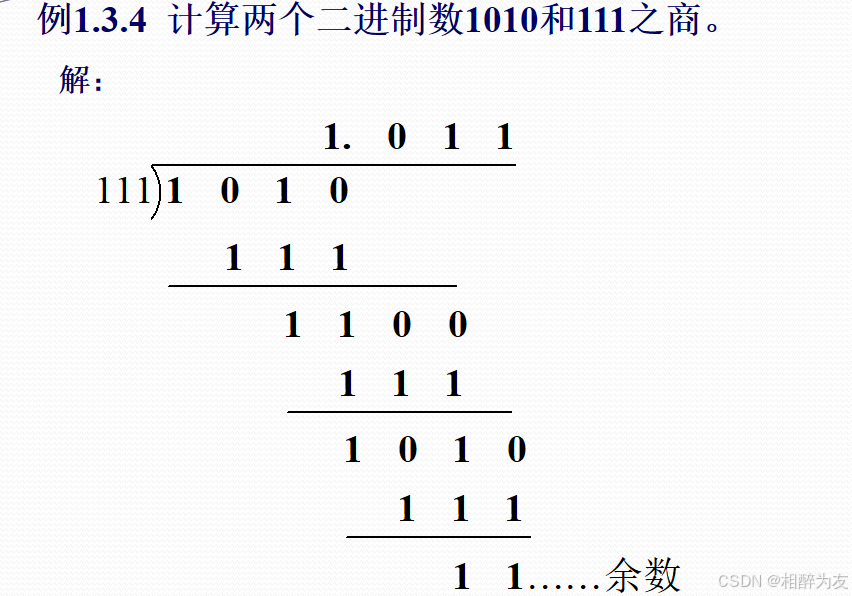
1、有符号二进制
1.有符号的二进制数表示 :
最高位表示符号位,且用0表示正数,用1表示负数。
其余部分为原码的形式表示数值位
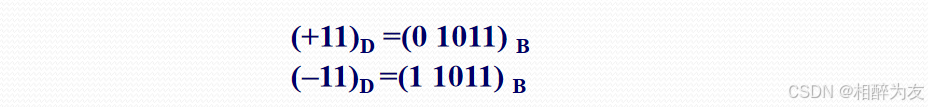
二进制数的补码表示:
补码或反码的最高位为符号位,正数为0,负数为1
当二进制数为正数时,其补码、反码与原码相同
当二进制数为负数时,将原码部分(不含符号位)逐位求反=反码,然后反码+1=补码。
| -6 | 1 1 1 0 | 1 0 0 1 | 1 0 1 0 |
| +6 | 0 1 1 0 | 0 1 1 0 | 0 1 1 0 |
2.二进制补码的运算
减法运算:
减法运算的原理:减去一个正数相当于加上一个负数A-B=A+(-B),对(-B)求补码,然后进行加法运算
公式:
A-B={(A+(B)补)+1}=(A-B)补//因为(A)补=A
#结果最高位舍弃 值得一提的是:
运算结果而然为补码
运算过程符号位也正常参与

图上运算结果超过了模而进位部分需要舍弃
这里的模是指技术系统的进位基数
二进制补码的减法运算意义:
在于简化了计算机的硬件设计,统一了运算规则,支持了有符号数的表示和处理,实现了高效的数值运算,消除了溢出问题,使得减法运算能够通过加法器实现,以及便于编程和算法的实现。这些特性使得补码成为现代计算机系统中不可或缺的一部分
溢出问题:
- 溢出定义:当计算结果超出了计算机能够表示的最大或最小值范围时,就会发生溢出。对于有符号数,这通常意味着结果超出了数据类型能够表示的最小负数或最大正数。
以至于符号位与进位冲突

解决溢出的办法:——位扩展!!
三个数据位不够就加几位
- 溢出的判别:
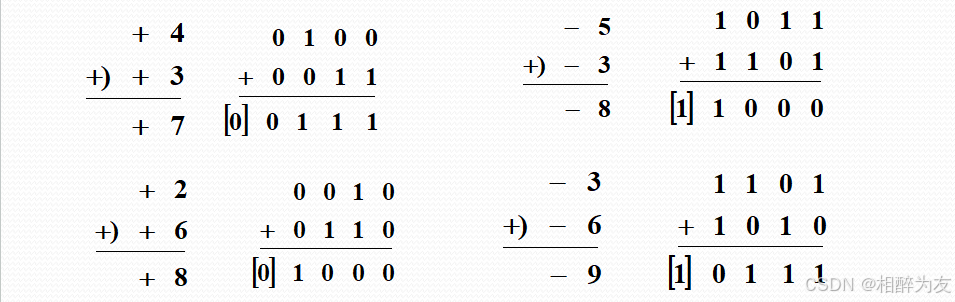
- 符号位比较法:如果两个符号相同的补码数相减,差的符号与减数的符号相同时,结果可能溢出。
- 进位标志法:在减法运算中,如果最高数值位向符号位送的进位值,与符号位送向更高位的进位值不同时,结果溢出。
- 双符号位法:在采用双符号位运算时,若两个符号位的值不同,则结果溢出。
实质就是判断有无进位动作
- 溢出处理:
计算机中一旦检测到溢出,通常需要采取特殊处理措施,如报错、截断结果或使用更宽的数据类型来避免数据丢失。
