在前文中我们学习了顺式二叉树的构建,现在我们来到链式二叉树的构建
在构建链式二叉树开始之前,需要对树及二叉树有一定的了解,如果有想要了解的可以移驾大该文
二叉树:堆的建立和应用_二叉堆的应用-CSDN博客
概念
链式二叉树是用链表来表示的一棵二叉树,也就是它的存储空间不是连续的
它的结点结构组成也和链表结点相似,由数据域和左右孩子节点指针域组成,由于二叉树的性质,每个父结点都会有0个或0个以上的孩子结点,但不多于两个,所以要有两个指向左右孩子结点的指针,指针类型和结点类型相同
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;//左孩子结点struct BinaryTreeNode* rigth;//右孩子结点}BTNode;也由于它链式结构的原因,它的元素插入没什么太大的意义,只要保证每个父结点的孩子结点个数不超过两个就行,所以在这里,我们就不对链式二叉树的结点插入做过多的描述
构建
遍历
二叉树的操作离不开遍历,链式二叉树的遍历方式有四种:前序遍历、中序遍历、后序遍历以及层序遍历
前序遍历
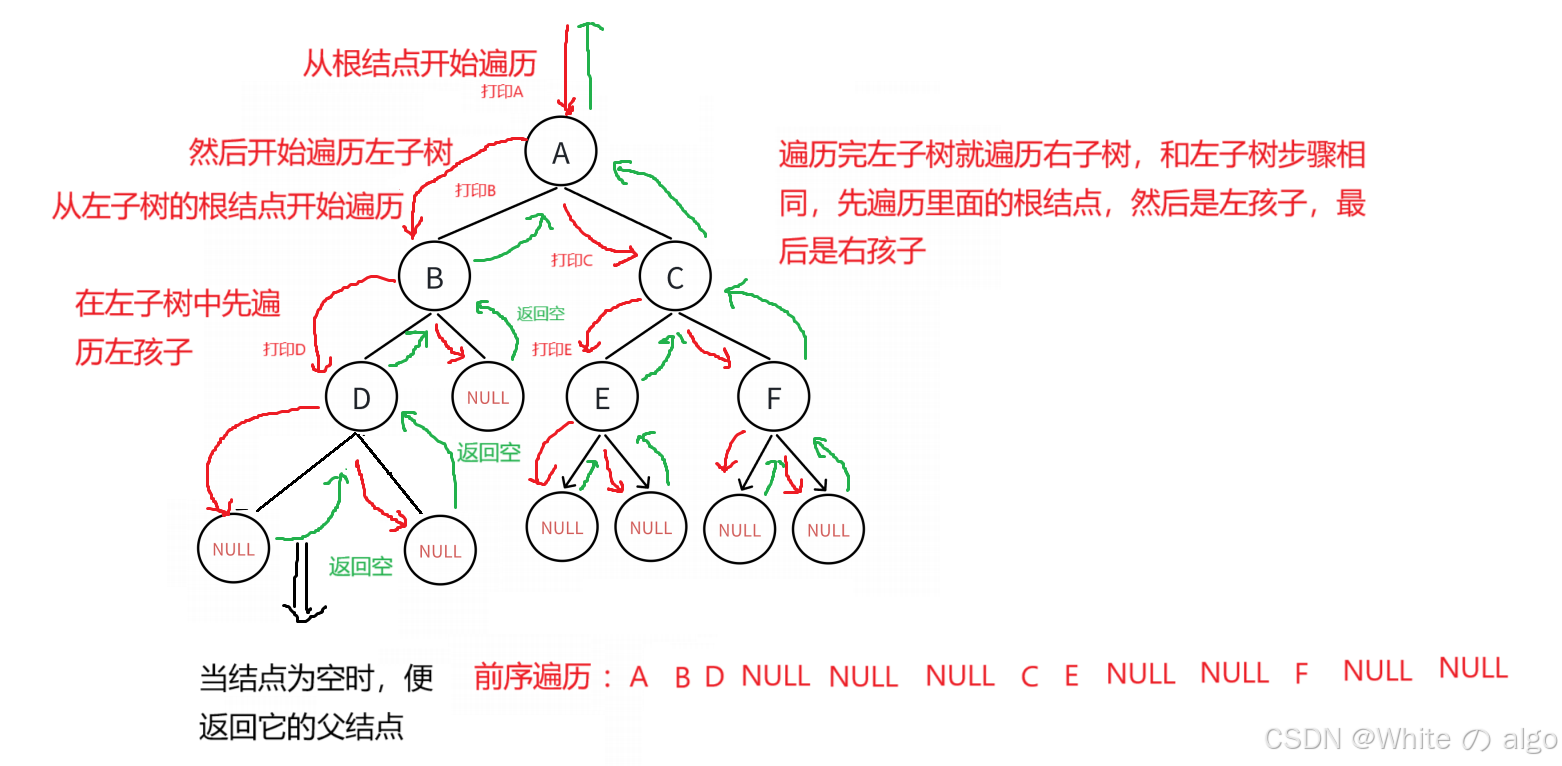
前序遍历又称为前根遍历,它的遍历方法是先遍历根结点,再左子树,最后右子树
而在遍历左子树时,先遍历父结点,在遍历左孩子,最后遍历右孩子
右子树也一样
遍历具体步骤思路如图所示:
思路得到了以后可得代码为:
//前序遍历:根->左->右(前根遍历)
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PreOrder(root->left);PreOrder(root->rigth);
}中序遍历
中序遍历又称中根遍历,由前边的前根遍历,我们也可以猜测到,它是先遍历左子树,在遍历根结点,最后遍历右子树
而在遍历左子树,先遍历里面的左孩子,在回来遍历父结点,最后遍历右孩子
右子树也是这样
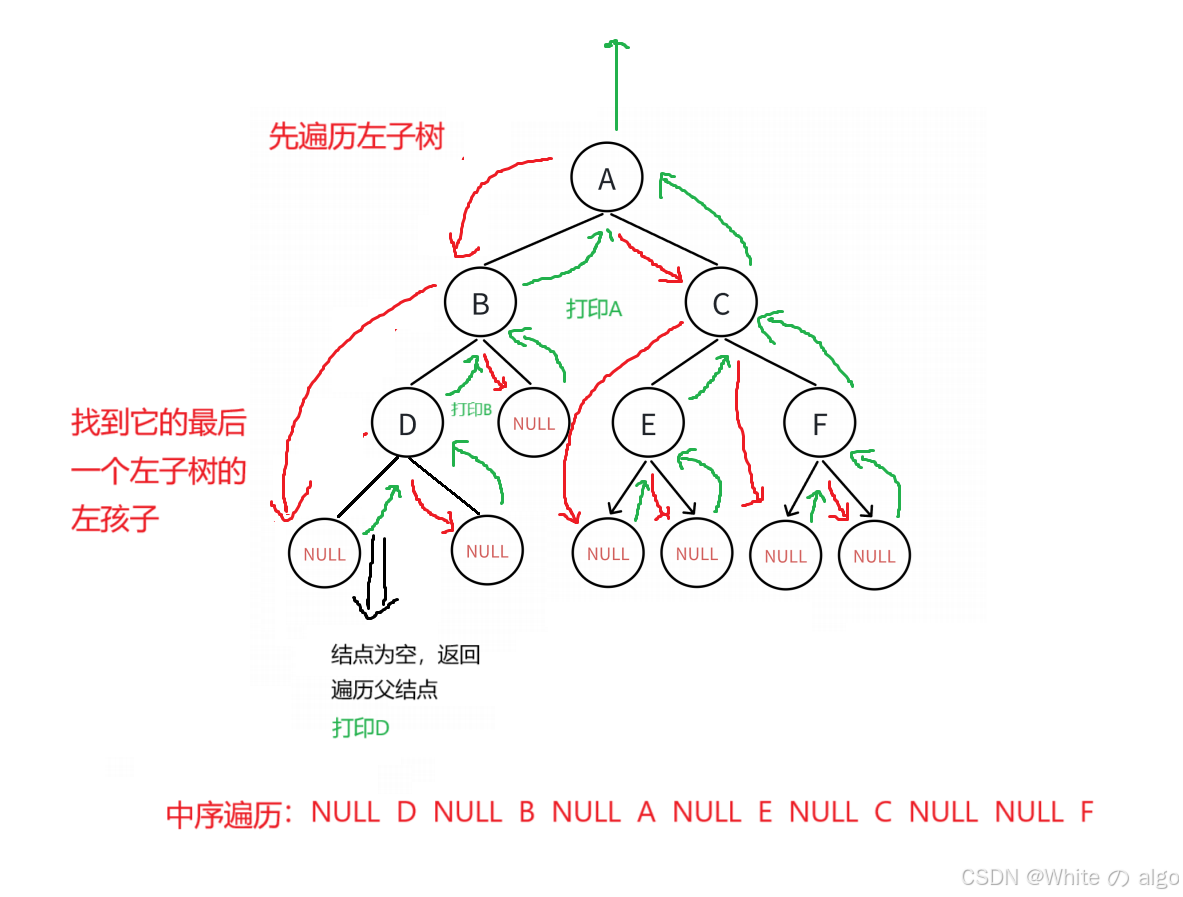
代码为:
//中序遍历:左->根->右(中根遍历)
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->rigth);
}后序遍历
后序遍历又称后根遍历,也就是这种遍历方法,最后遍历根结点,先遍历左子树,再遍历右子树
先遍历左子树的左孩子,在遍历右孩子,最后遍历父结点
右子树相同
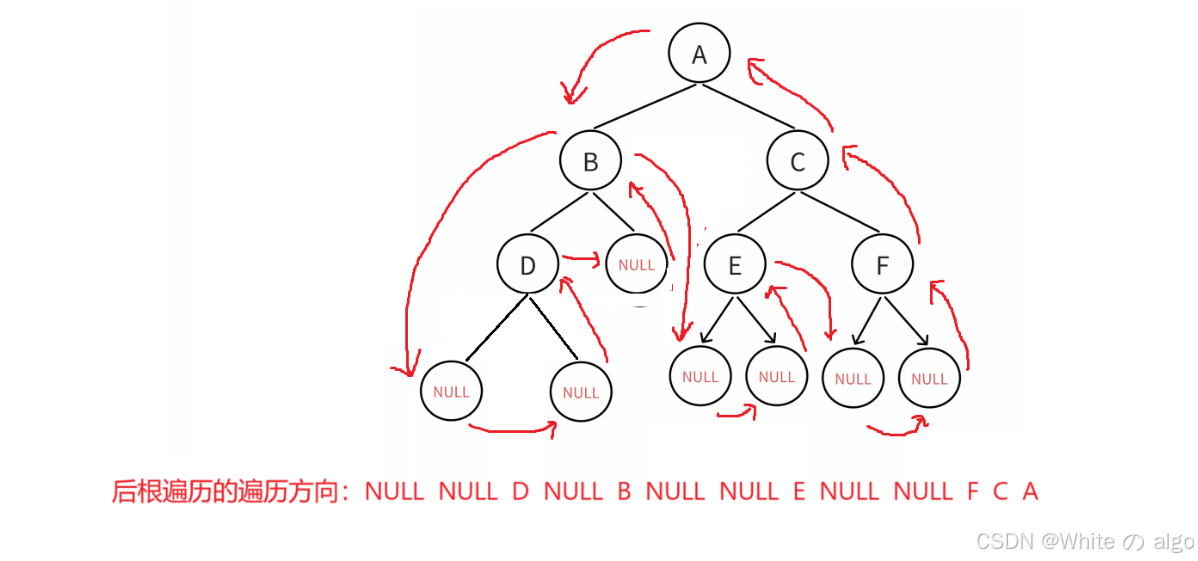
代码为:
//后序遍历:左->右->根(后根遍历)
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->rigth);printf("%c ", root->data);
}层序遍历
该遍历方法和前面三种方法不同,因为它是一层一层的遍历二叉树,这种方法就不需要用到递归
它要用到队列的数据结构,在这里的入队列的元素类型为链式二叉树的结点类型
借助队列的先进先出的特性,先将根结点入队列再出队列,然后判断它是否有左右孩子,有的话,就将左右孩子入队列,依次循环入队列、出队列,直到队列为空
注:
在队列的数据结构中需要将将元素类型改为链式二叉树结点类型,在声明时要将struct关键字加上
这里就涉及到前置声明:要告诉当前文件,在某个文件中存在这个结构体,却不需要告诉在哪个文件中,当然必须声明为结构体
/*当前文件为队列的头文件*///将这里的队列元素类型改为二叉树结点类型:用指针
typedef struct BinaryTreeNode* QDataType;
//typedef struct BTNode* QDataType;//这里用到前置声明:struct可以用于在其他文件中声明,告诉这个文件会有一个这样名字的结构体
//之所以用指针,是因为在传入队列中的元素类型时二叉树的结点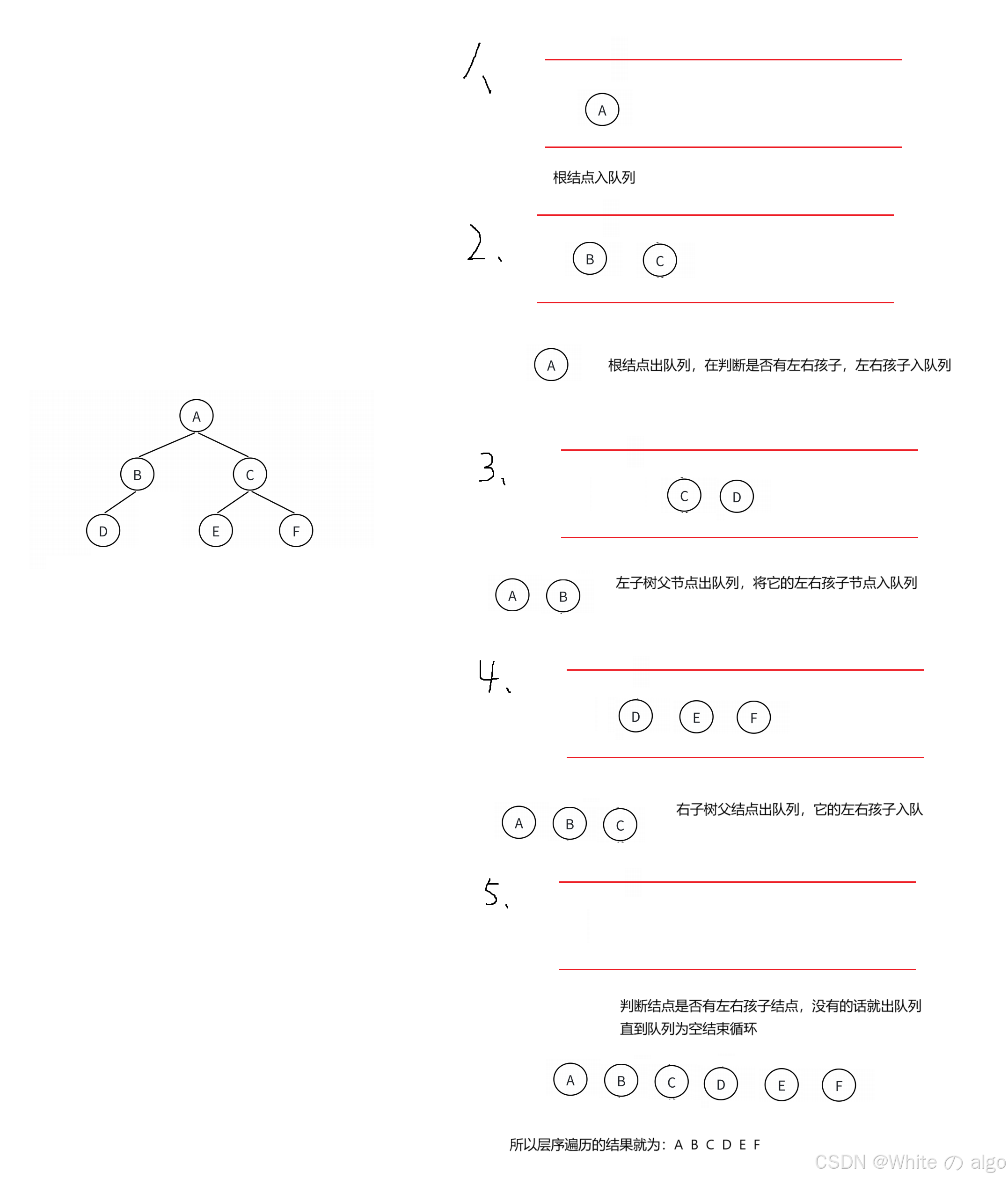
代码为:
//层序遍历:这里要用到队列,通过队列将二叉树中的结点一个一个拿出来排序
/*
思路:根结点入队列,再出队列,然后判断根结点是否有左右结点,将左右结点入队循环上述步骤直到队列为空(结束条件)*/
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//初始化QPushBack(&q, root);while (!QueueEmpty(&q))//队列不为空{BTNode* top = QueueFront(&q);//取队头QPopFront(&q);//出队列printf("%c ", top->data);if (top->left){QPushBack(&q, top->left);}if (top->rigth){QPushBack(&q, top->rigth);}}QueueDestroy(&q);//销毁(有借有还)
}二叉树结点个数
二叉树的结点个数 = 根结点个数 + 左子树结点个数 + 右子树结点个数
我们已知根结点就只有一个,而当结点为空的时候就返回0,由此依次递归下去
代码为
// ⼆叉树结点个数:1(根结点个数)+左子树结点个数+右子树结点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->rigth);
}二叉树叶子结点个数
二叉树叶子结点个数 = 左子树叶子结点个数 + 右子树叶子结点个数
已知当结点的左右结点都为空就是叶子结点,满足这个条件就返回1,为空就返回0,依次遍历下去
代码为:
// ⼆叉树叶⼦结点个数:左子树叶子结点个数+右子树结点个数
//当结点的左右孩子节点都为NULL时就为叶子结点
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->rigth == NULL){return 1;}return BinaryTreeLeafSize(root->rigth) + BinaryTreeLeafSize(root->left);}二叉树第k层结点个数
⼆叉树第k层结点个数 = 当k==1时当前层数左右子树结点个数之和
每调用一次函数k--,当就k==1时,就是到了要求的层次,遍历这一层的左子树,再遍历右子树
最后将两边的结点数相加
//⼆叉树的深度/⾼度:根结点层次+左右子树中最大的层次
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftdep = BinaryTreeDepth(root->left);int rigthdep = BinaryTreeDepth(root->rigth);return 1 + (leftdep > rigthdep ? leftdep : rigthdep);
}二叉树查找值为x的结点
遍历方法为:先遍历右子树,如果找了就直接返回(不需要再继续递归下去了);没有的话,就遍历右子树
当遍历到的结点为空的时候,就返回;当有重复的值,就返回第一个遍历到的结点
代码为:
// ⼆叉树查找值为x的结点:先遍历左子树,如果找到了就直接返回,否则就遍历右子树
//当树中有重复值时,就返回第一个结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return;}if (root->data == x){return root;}BTNode* leftfind = BinaryTreeFind(root->left, x);if (leftfind){return root->left;}BTNode* rigthfind = BinaryTreeFind(root->rigth, x);if (rigthfind){return root->rigth;}
}
二叉树销毁
销毁这一步骤这里就用后序遍历,又因为要连同根结点一起销毁,所以这里用二级指针
具体步骤和后序遍历大致相同,就是将打印结点值这一步改为free,然后将指针置空
// ⼆叉树销毁:这里用后序遍历,因为要将连同根结点一起销毁,所以用二级指针
void BinaryTreeDestory(BTNode** root)
{if ((*root) == NULL){return;}BinaryTreeDestory((&(*root)->left));BinaryTreeDestory((&(*root)->rigth));free(*root);*root = NULL;
}判断二叉树是否为完全二叉树
判断二叉树是否为完全二叉树中也和层序遍历一样,要用到队列的数据结构
思路为:
将根结点入队列,再出队列
然后将根结点的左右孩子结点入队列,
当入队列的结点为空的时候就结束循环
第一次循环结束后,队列中可能还会有元素,所以需要进行第二次循环
完全二叉树:
第二次循环中队列剩下所有结点都为空
非完全二叉树:
第二次循环中队列剩下结点有不为空
第二次循环中当出现结点不为空就结束循环
非往前二叉树判断步骤:
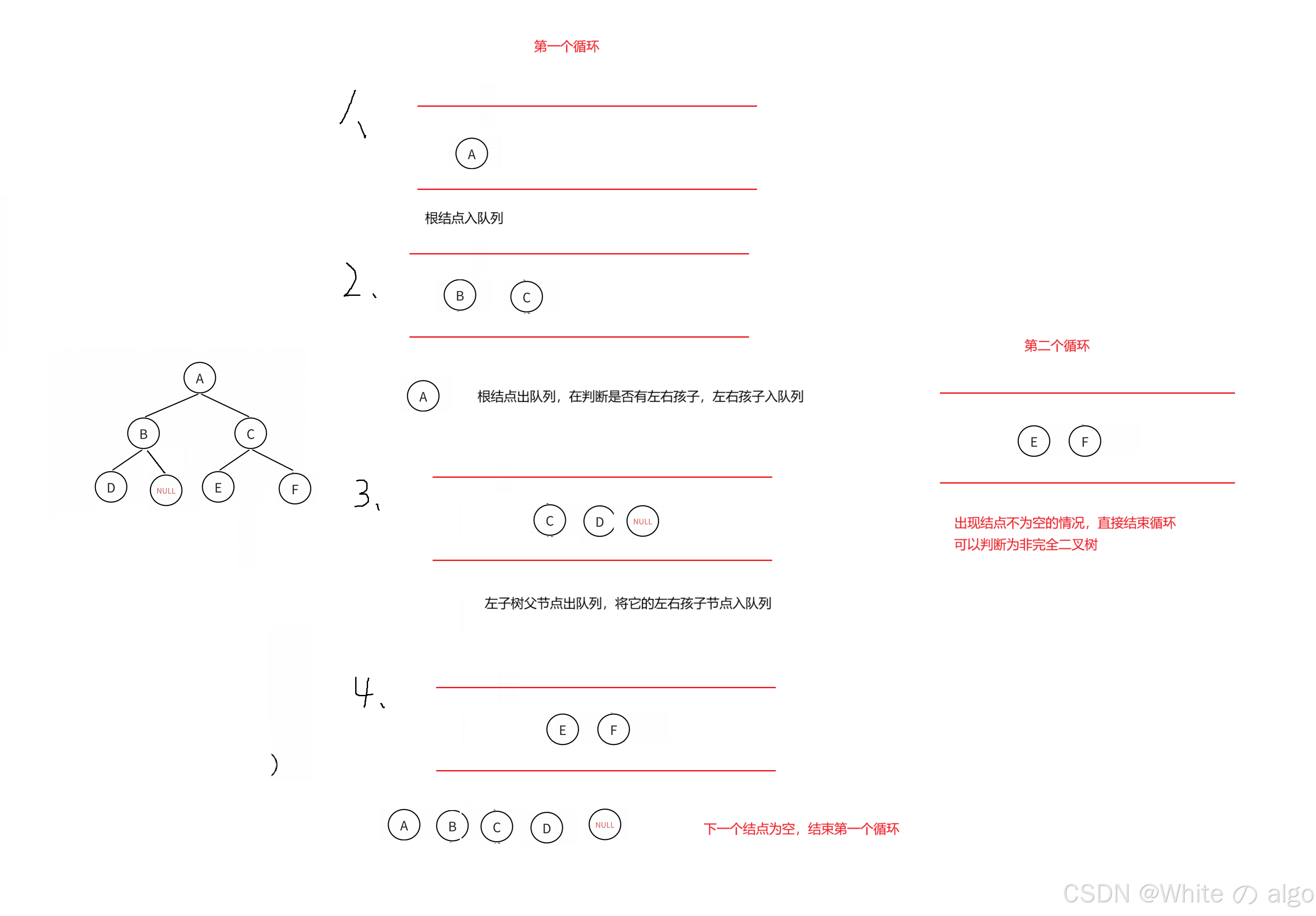
完全二叉树判断步骤:
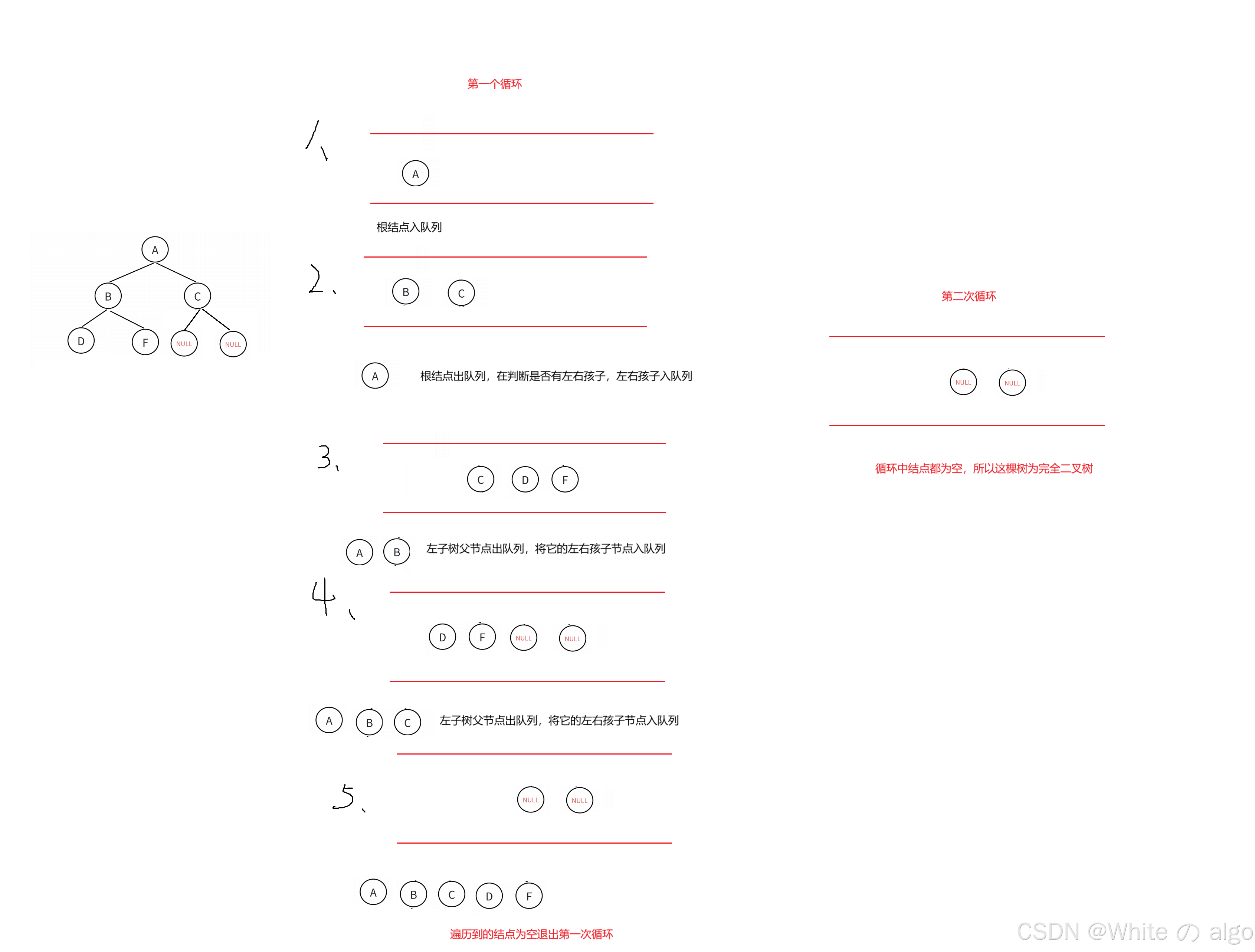 代码为:
代码为:
//判断二叉树是否为完全二叉树
/*思路:使用队列的数据结构将根结点入队列,再出队列然后将根结点的左右孩子结点入队列,当入队列的结点为空的时候就结束循环第一次循环结束后,队列中可能还会有元素,所以需要进行第二次循环完全二叉树:第二次循环中队列剩下所有结点都为空非完全二叉树:第二次循环中队列剩下结点有不为空第二次循环中当出现结点不为空就结束循环
*/
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QPushBack(&q, root);//入队列while (!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QPopFront(&q);//出队列if (top==NULL){break;}QPushBack(&q, top->left);QPushBack(&q, top->rigth);}while (!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QPopFront(&q);//出队列if (top != NULL){QueueDestroy(&q);//销毁return false;}}QueueDestroy(&q);return true;
}至此,链式二叉树的构造就完成了
