K-Means算法详解与实战应用.

在数据分析的众多工具中，K-Means聚类算法以其简单、直观和高效的特点，成为了探索数据集结构的常用方法。本文将带你深入了解K-Means算法的原理，并展示如何在实际项目中运用这一强大的聚类工具。

一 算法原理

K-Means是一种迭代聚类算法，其目标是将n个点划分为K个聚类，每个点属于最近的聚类中心的聚类。。K-means算法实现步骤如下：

输入：数据集$D = { {x_1},{x_2}, \cdots ,{x_n}} $，聚类个数$k$
输出：聚类结果类簇

1. **初始化：**随机初始化$k$个样本作为聚类中心 { μ 1 , μ 2 , ⋯ , μ k } \{ {\mu _1},{\mu _2}, \cdots ,{\mu_k}\} {μ1​,μ2​,⋯,μk​}；

2. **分配：**计算数据集中所有样本$x_i$到各个聚类中心${\mu }_j$的距离$dist(x_i,{\mu }_j)$，并将$x_i$划分到距离最小的聚类中心所在类簇中；

3. 更新：对于每一个类簇，更新其聚类中心：${\mu }_i=\frac{1}{|c_i|}\sum _{x\in c_i}x$

4. 迭代：重复2,3步骤，直到聚类中心不再有明显变化或满足迭代次数。

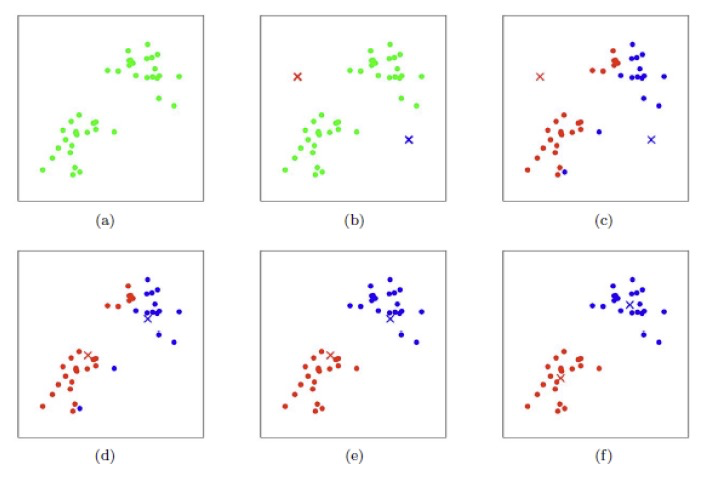
总结而言，K-means算法整个流程可总结为一个优化问题，通过不断迭代使得目标函数收敛，K-means算法目标函数为：
$$J={\sum }_{j=1}^k{\sum }_{i=1}^{n}dist(x_i,{\mu }_j)$$
从目标函数中可以看出，有两个因素对聚类结果有着至关重要的影响：$k$值、距离度量方式。

对于距离度量方式，请查看往期文章：机器学习中的聚类艺术：探索数据的隐秘之美

对于k值，常采用肘部法则。

二 实战演练：使用Python实现K均值聚类

为了让大家更好地理解K均值算法的实际应用，我们将通过一个简单的Python代码示例来演示整个过程。这里我们使用Scikit-Learn这个强大的机器学习库。

1. 安装必要的库：

   pip install numpy matplotlib scikit-learn
   

2. 导入库并生成模拟数据：

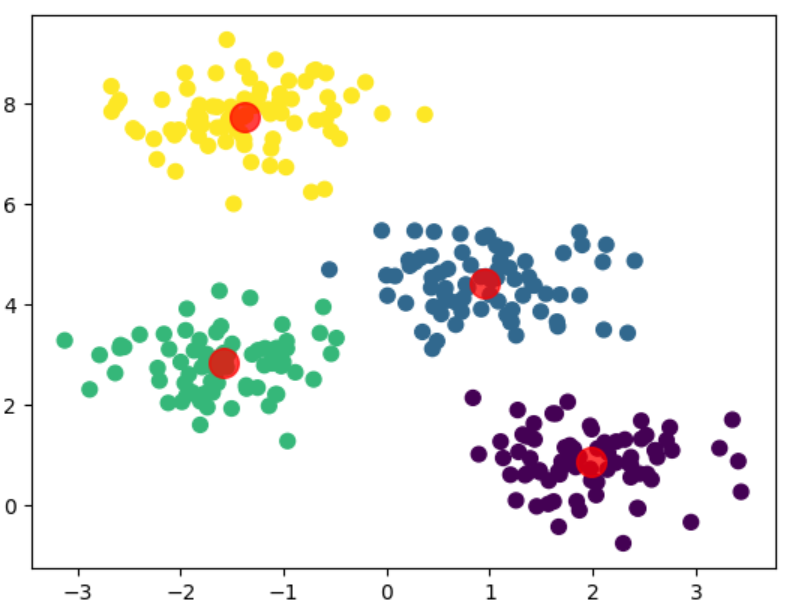
   import numpy as np
   from sklearn.cluster import KMeans
   from sklearn.datasets import make_blobs
   import matplotlib.pyplot as plt# 生成模拟数据
   X, _ = make_blobs(n_samples=300, centers=4, random_state=0, cluster_std=0.6)
   

3. 执行K均值聚类：

   kmeans = KMeans(n_clusters=4)
   kmeans.fit(X)
   y_kmeans = kmeans.predict(X)
   

4. 可视化结果：

   plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')centers = kmeans.cluster_centers_
   plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75);
   plt.show()
   

三 K均值算法的优点与局限

优点：

• 算法简单易实现。
• 运行速度快，适合大规模数据集。
• 可以处理多维数据。

局限：

• 需要预先指定簇的数量K，这在实际问题中并不总是可行。
• 对异常值敏感，可能会导致质心偏离。
• 假设簇是凸形的，对于复杂形状的簇效果不佳。