理解
机器学习可以理解为从数据中找出规则
如何找: 通过反馈机制(训练)找到规律
反馈机制的核心: 利用 数学+程式=Model 进行训练判定 从而使得有一定的正确率
简单线性回归
y_pred=w*x+b
利用绘图工具 pyplot 绘制数据图像
import pandas as pd
import matplotlib.pyplot as pltfrom types import FrameType
import matplotlib as mlp
from matplotlib.font_manager import fontManager
fontManager.addfont("ChineseFont.ttf")
mlp.rc('font',family="ChineseFont")url="https://raw.githubusercontent.com/GrandmaCan/ML/main/Resgression/Salary_Data.csv"
data = pd.read_csv(url)x=data["YearsExperience"]
y=data["Salary"]
plt.scatter(x, y,marker="x",color="red")
plt.title("年资-薪水")
plt.xlabel("年资")
plt.ylabel("月薪(千)")
plt.show()可完善定义函数
def plot_pred(w,b):y_pred=x*w+bplt.plot(x,y_pred,color="blue",label="预测系")plt.scatter(x,y,marker="x",color="red",label="真实数据")plt.title("年资-薪水")plt.xlabel("年薪")plt.ylabel("月薪(千)")plt.xlim([0,12])plt.ylim([-60,140])plt.legend()plt.show()plot_pred(0,0)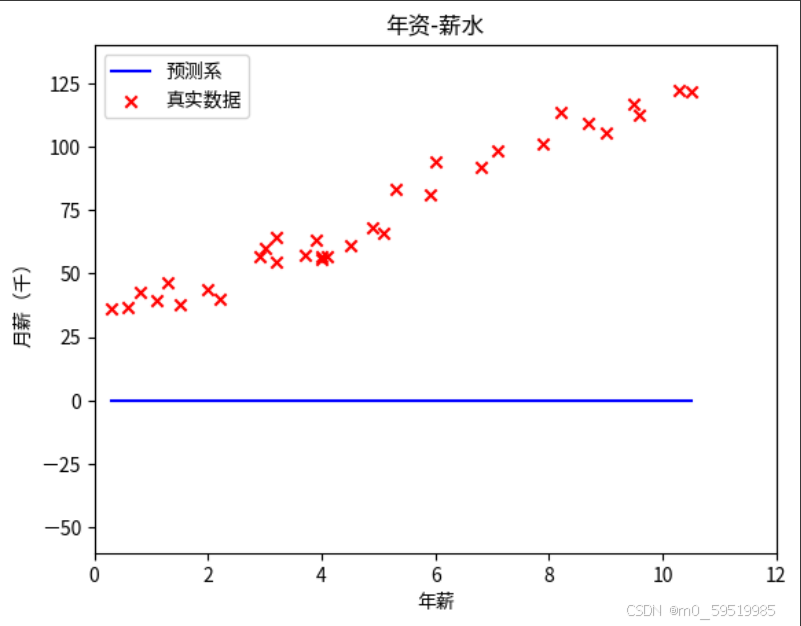
智能化调节
from ipywidgets import interact
interact(plot_pred,w=(-100,100,1),b=(-100,100,1))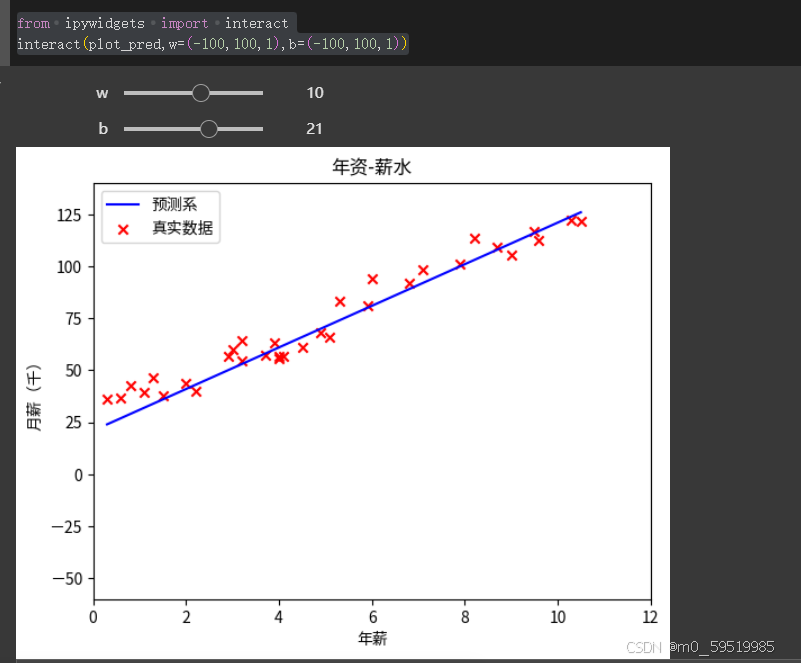
中文资源下载
!pip install wget
import wget
wget.download("https://github.com/GrandmaCan/ML/raw/main/Resgression/ChineseFont.ttf")对不同的预测直线进行评分:
成本函数cost
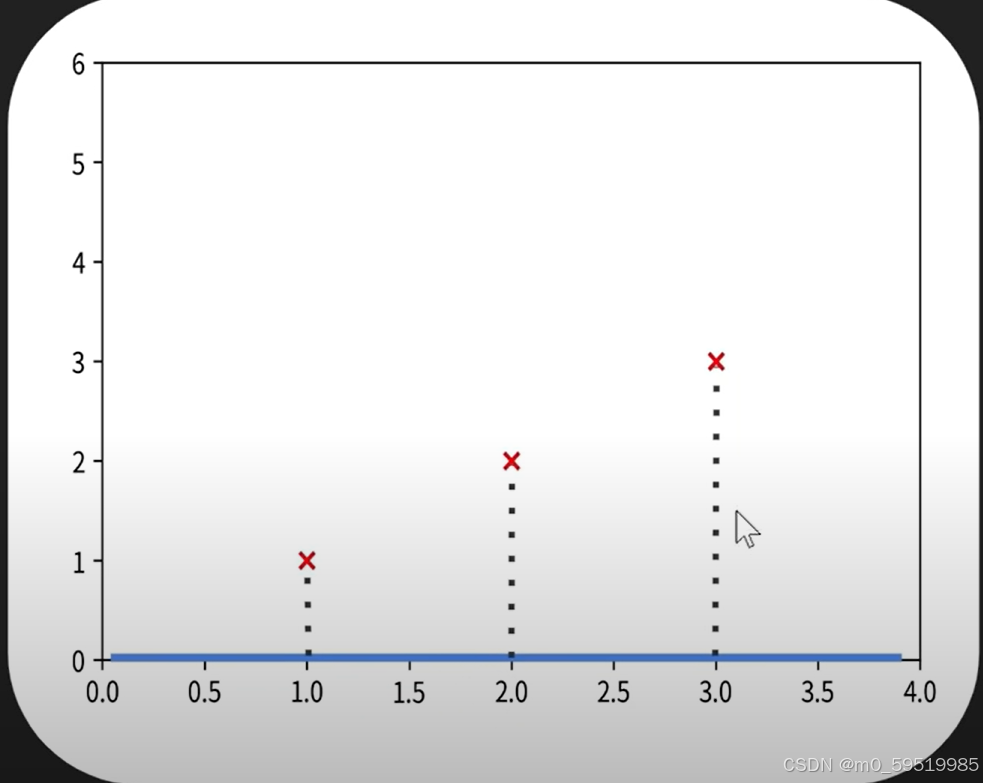
cost=(真实数据-预测值)^2 平方使对负数的处理更加方便,由图可知距离的平方的加总越小,cost最小的预测越准确,下面会对范围内的每一个w,b进行计算得到cost,并用二维矩阵进行展示
def compute_cost(x,y,w,b):y_pred=w*x+bcost=(y-y_pred)**2cost=cost.sum()/len(x)return cost# b=0 w= -100--100 cost会是多少
costs=[]
for w in range(-100,101):cost =compute_cost(x,y,w,0)costs.append(cost)
costs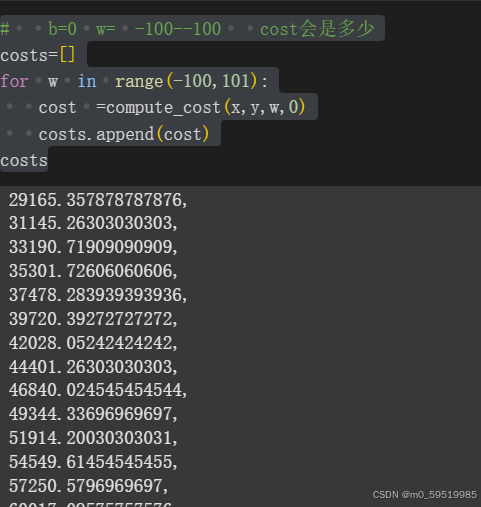
画图工具展示cost
import matplotlib.pyplot as plt
plt.scatter(range(-100,101),costs)
# plt.plot(range(-100,101),costs)
plt.title("cost function b=0 w-100~100")
plt.xlabel("w")
plt.ylabel("cost")
plt.show()可以使用numpy进行矩阵的运算
# w=-100~100 b=-100~100 的cost
import numpy as np
ws = np.arange(-100,101)
bs = np.arange(-100,101)
costs=np.zeros((201,201))i=0
for w in ws:j=0for b in bs:cost = compute_cost(x,y,w,b)costs[i,j]=costj=j+1i=i+1
costs此处介绍一下numpy,具体使用的方法可以去查询:
NumPy是Python中非常重要的库,主要用于处理数组和矩阵运算。用户可能知道Python的列表,但NumPy的数组在性能上有很大优势,特别是在处理大规模数据时。我需要强调这一点,同时提到它支持多维数组和数学函数,这对科学计算非常关键。
接下来,用户可能需要了解核心功能,比如创建数组、数组操作、数学运算、广播机制等。这些都是NumPy的基础,必须涵盖。另外,可能还要提到它与其他库(如Pandas、SciPy)的关系,以及它在机器学习中的应用,比如TensorFlow和PyTorch底层都使用类似NumPy的数组结构。
用户可能对性能比较感兴趣,比如为什么用NumPy而不是原生Python列表,这时候需要解释向量化操作和底层C实现的优势。同时,广播机制可能是一个复杂的概念,需要用简单的例子说明。
还要注意用户可能是在学习过程中遇到具体问题,比如数组形状操作或数学函数的使用,所以举一些实际的代码示例会有帮助。
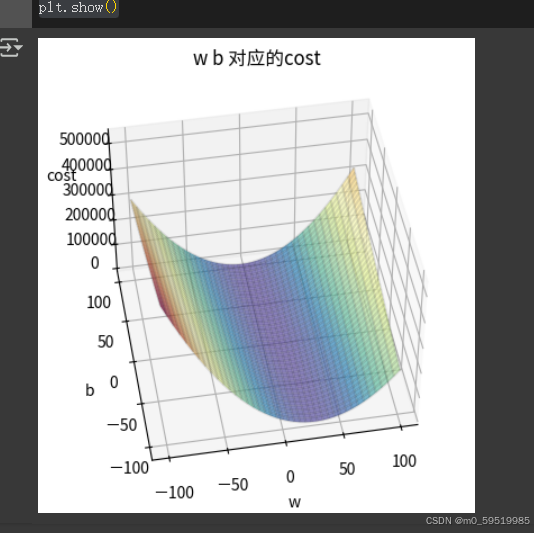
因为要同时考虑到w,b的值,可以对该二维矩阵costs进行3d展示:
from types import FrameType
import matplotlib as mlp
from matplotlib.font_manager import fontManager
fontManager.addfont("ChineseFont.ttf")
mlp.rc('font',family="ChineseFont")ax=plt.axes(projection="3d")
ax.view_init(45,-100) #第一参数是图像上下旋转,第二个是左右旋转
# ax.xaxis.set_pane_color((0,0,0))
# ax.yaxis.set_pane_color((0,0,0))
# ax.zaxis.set_pane_color((0,0,0))b_grid,w_grid= np.meshgrid(bs,ws)# cmap设置一个色彩
ax.plot_surface(w_grid,b_grid,costs,cmap="Spectral_r",alpha=0.7)
#设置图像边框
ax.plot_wireframe(w_grid,b_grid,costs,color="black",alpha=0.1)
ax.set_title("w b 对应的cost")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")
plt.show()其中用到了meshgrid()进行二维网格的绘制,meshgrid()方法接受两个一维向量,生成一个坐标矩阵。具体的实现与理解可参考以下资料:
理解numpy中的meshgrid()方法 | 田野光的技术小站
注:此外该网站还有其他一些机器学习知识点的清晰解答
找出最小的cost,并在图中标出
from types import FrameType
import matplotlib as mlp
from matplotlib.font_manager import fontManager
fontManager.addfont("ChineseFont.ttf")
mlp.rc('font',family="ChineseFont")plt.figure(figsize=(7,7))
ax=plt.axes(projection="3d")
ax.view_init(45,-100) #第一参数是图像上下旋转,第二个是左右旋转
# ax.xaxis.set_pane_color((0,0,0))
# ax.yaxis.set_pane_color((0,0,0))
# ax.zaxis.set_pane_color((0,0,0))b_grid,w_grid= np.meshgrid(bs,ws)# cmap设置一个色彩
ax.plot_surface(w_grid,b_grid,costs,cmap="Spectral_r",alpha=0.7)
#设置图像边框
ax.plot_wireframe(w_grid,b_grid,costs,color="black",alpha=0.1)
ax.set_title("w b 对应的cost")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")w_index,b_index=np.where(costs==np.min(costs))
print(f"当w={ws[w_index]},b={bs[b_index]} 会有最小cost:{costs[w_index,b_index]}")
ax.scatter(ws[w_index],bs[b_index],costs[w_index,b_index],color="red")plt.show()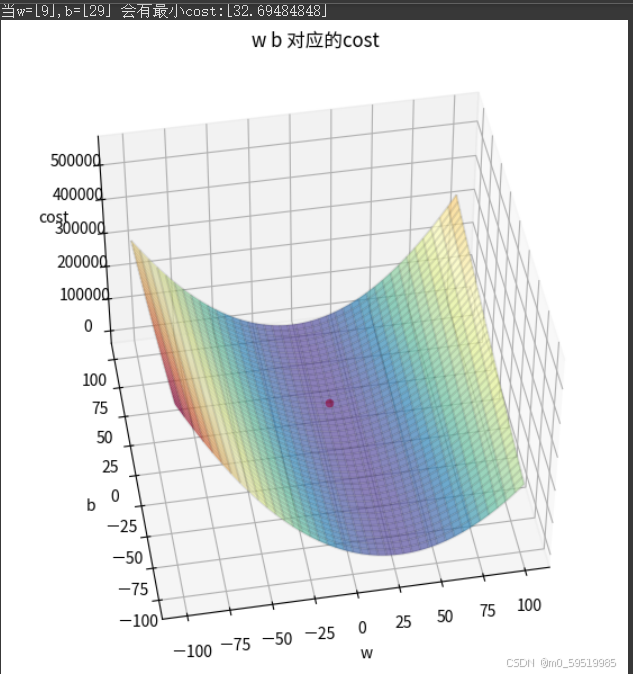
如何高效找出cost
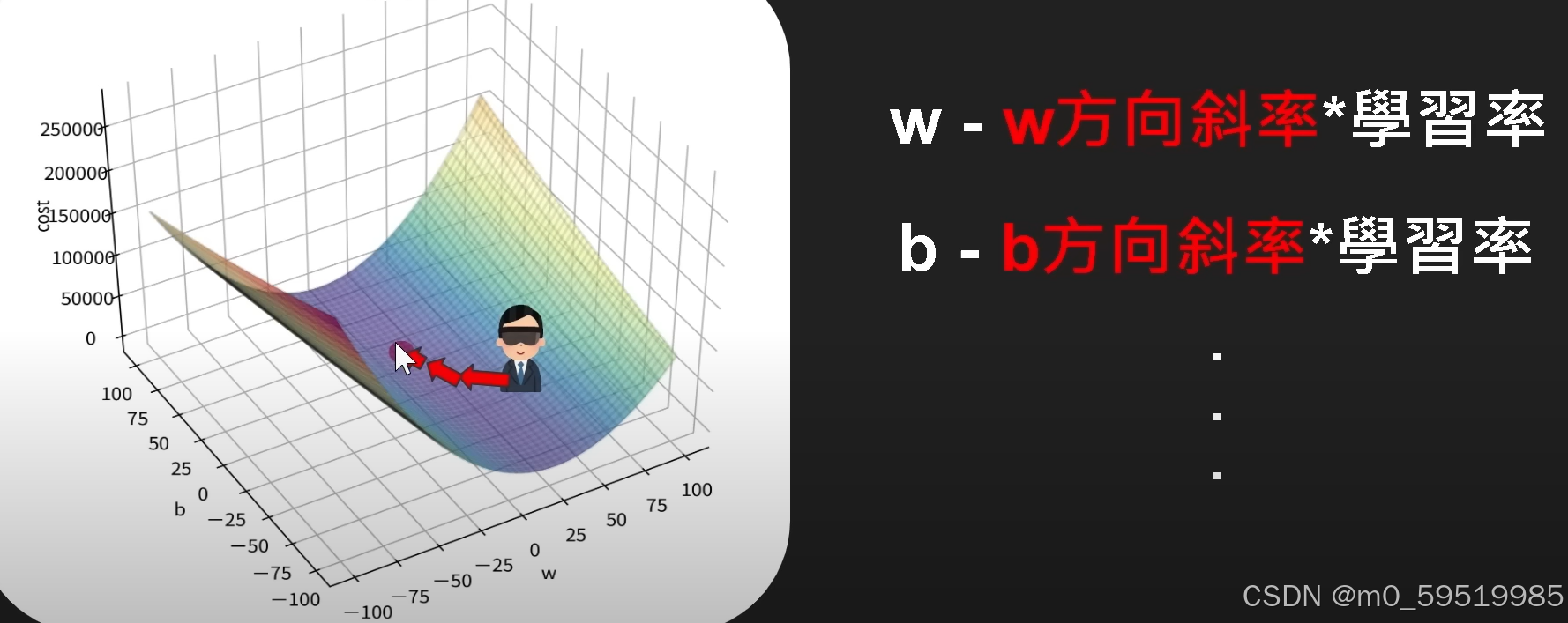
使用穷举的方法找出cost效率太低了,可以使用gradient descent (梯度下降)
gradient descent
=根据斜率改变参数 w,b
可以使用微分的方法测定没一点的斜率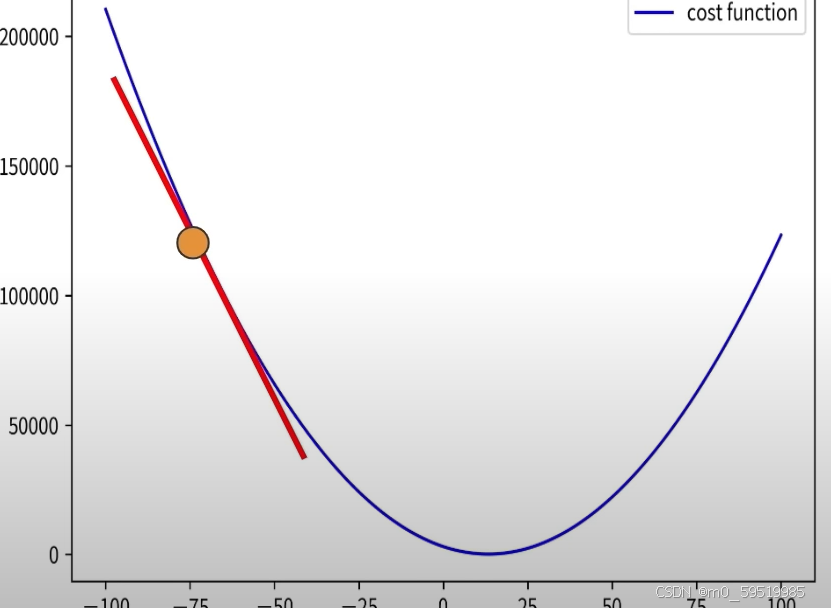
(真实数据-预测数据)的平方
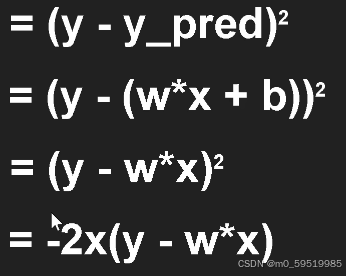
不断更新斜率

学习率
其中学习率即梯度下降的步伐大小,自己去设定
若学习率过大(以b=0的情况为例),则会出现:
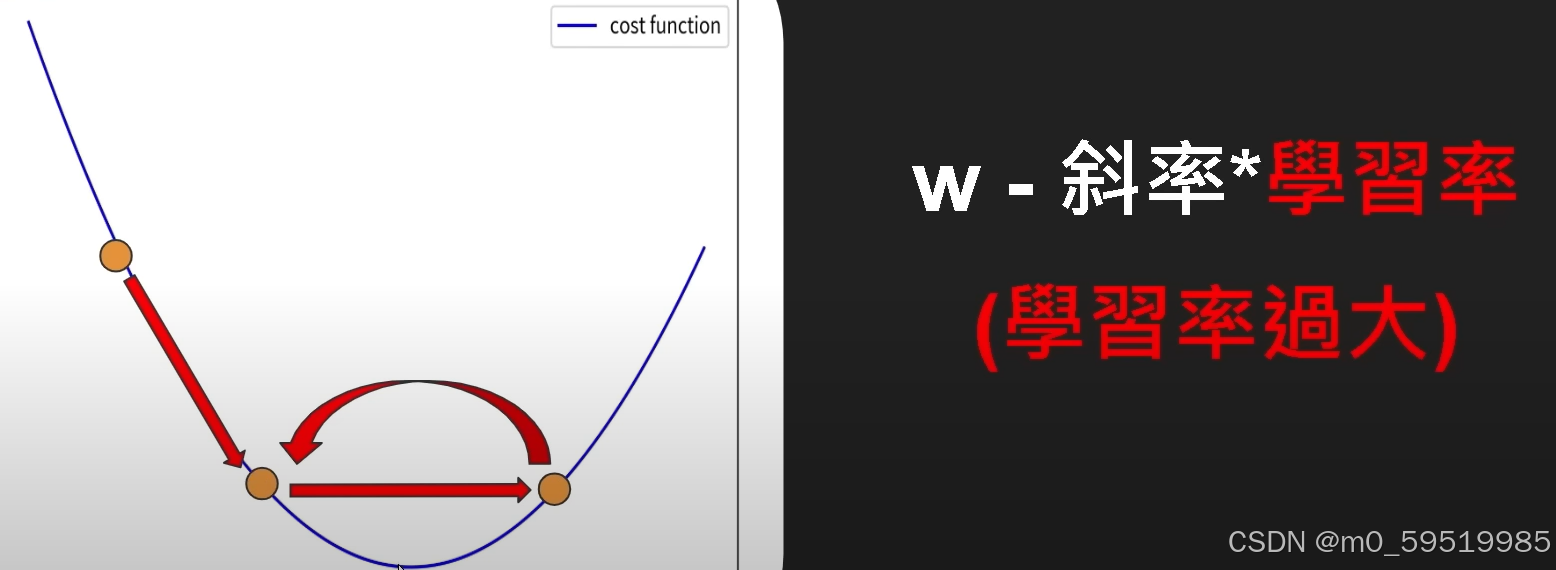
若学习率过小,则:
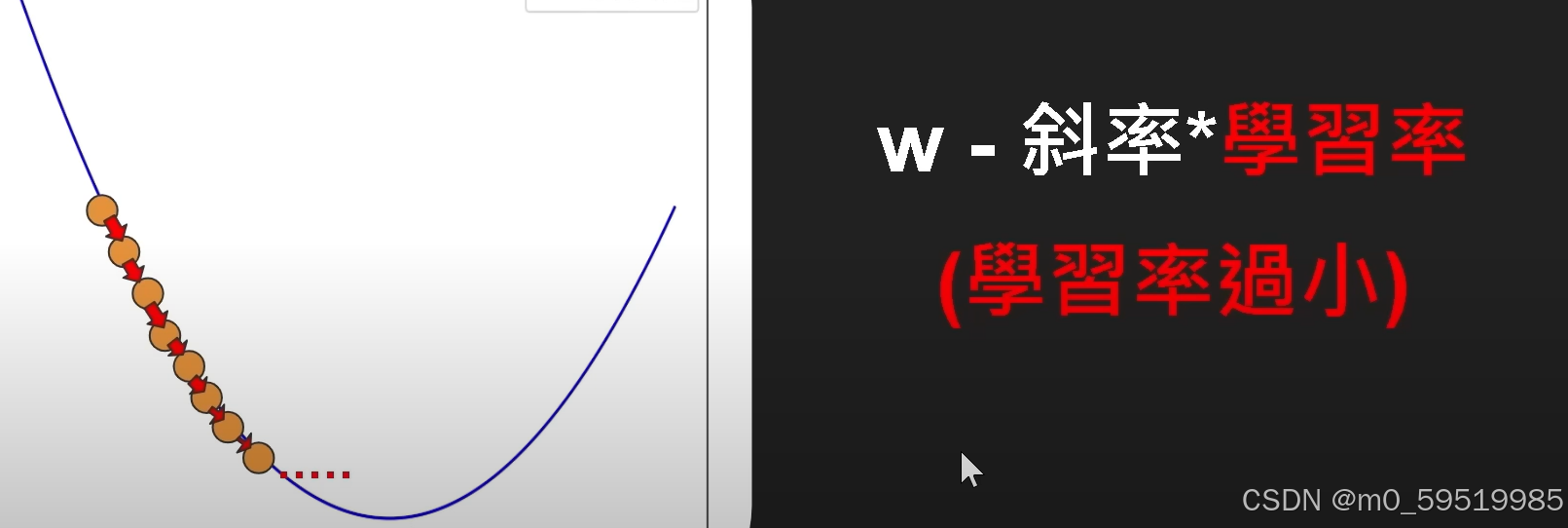
通过不断地实验测试来测定合适的学习率
同理,b!=0的情况来看
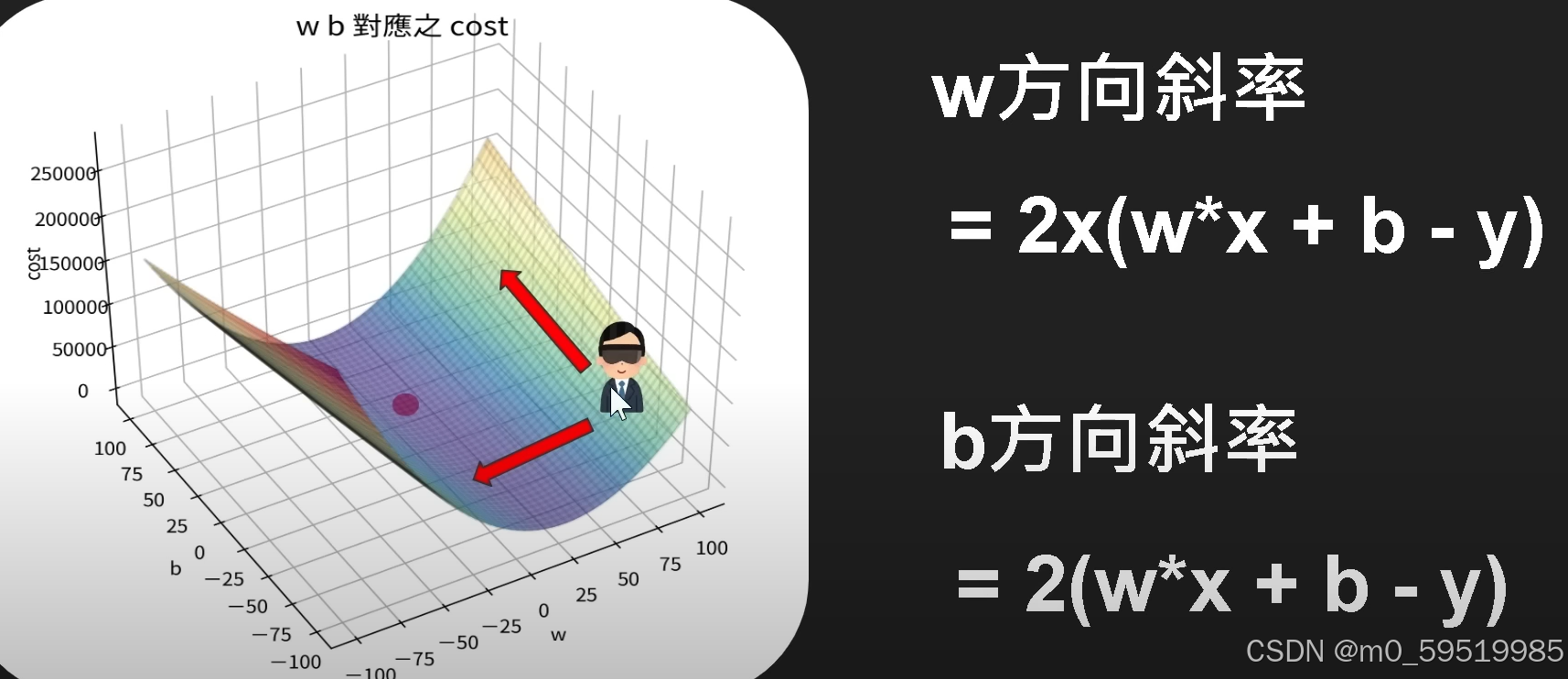
同理,学习率过大过小都可能造成相应的问题出现
计算w,b方向的斜率
def compute_gradient(x,y,w,b):w_gradient = (2*x*(w*x+b-y)).mean()b_gradient = (2*(w*x+b-y)).mean()return w_gradient,b_gradient由w,b方向的梯度更新w,b
其中学习率经过测试选择0.001效果会更好
w=0
b=0
learning_rate=0.001
w_gradient,b_gradient=compute_gradient(x,y,w,b)w=w-w_gradient*learning_rate
b=b-b_gradient*learning_rate
w,b之后我们可以看下cost有没有下降
w=0
b=0
learning_rate=0.001
w_gradient,b_gradient=compute_gradient(x,y,w,b)
print(compute_cost(x,y,w,b))
w=w-w_gradient*learning_rate
b=b-b_gradient*learning_rate
print(compute_cost(x,y,w,b))
w,b或者梯度可以不乘2,学习率变成0.002效果是相同的
找出最小cost
使用梯度下降的方法,不断更新w,b,并计算cost的值,最后可以封装成一个函数
def gradient_descent(x, y, w_init, b_init, learning_rate, compute_cost, compute_gradient, run_iter, p_iter=1000):# 初始化参数历史记录列表w_hist = []b_hist = []cost_hist = []# 初始化参数w = w_initb = b_initfor i in range(run_iter):# 计算梯度w_gradient, b_gradient = compute_gradient(x, y, w, b)# 更新参数w = w - w_gradient * learning_rateb = b - b_gradient * learning_rate# 计算成本cost = compute_cost(x, y, w, b)# 记录参数和成本w_hist.append(w)b_hist.append(b)cost_hist.append(cost)# 每 p_iter 次迭代打印一次信息if (i % p_iter == 0):print(f"Iteration {i:5}, Cost {cost:.4e}, w: {w:.4e}, b: {b:.4e}")return w, b, w_hist, b_hist, cost_hist给定w,b初始值均为0,学习率为0.001,运行3万次
w_init=0
b_init=0
learning_rate=1.e-3
run_iter=30000
w_final,b_final,w_hist,b_hist,cost_hist=gradient_descent(x,y,w_init,b_init,learning_rate,compute_cost,compute_gradient,run_iter) 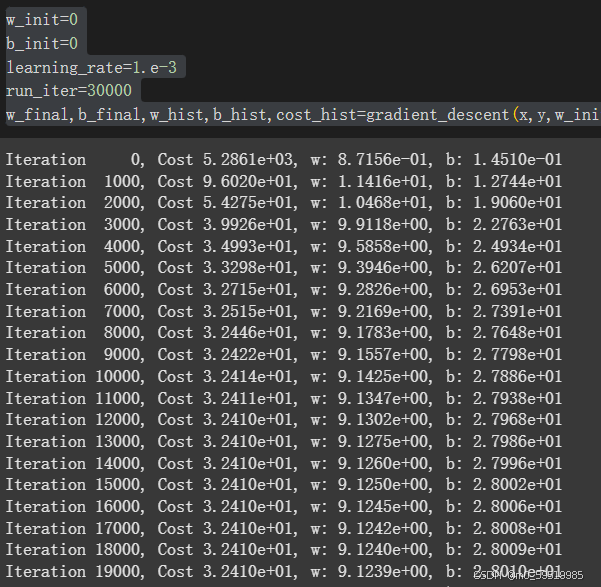
我们可以看到当w,b给定时,使用梯度下降算法,cost的值在下降,w在下降,b在升高
再打印出w,b方向下降的梯度
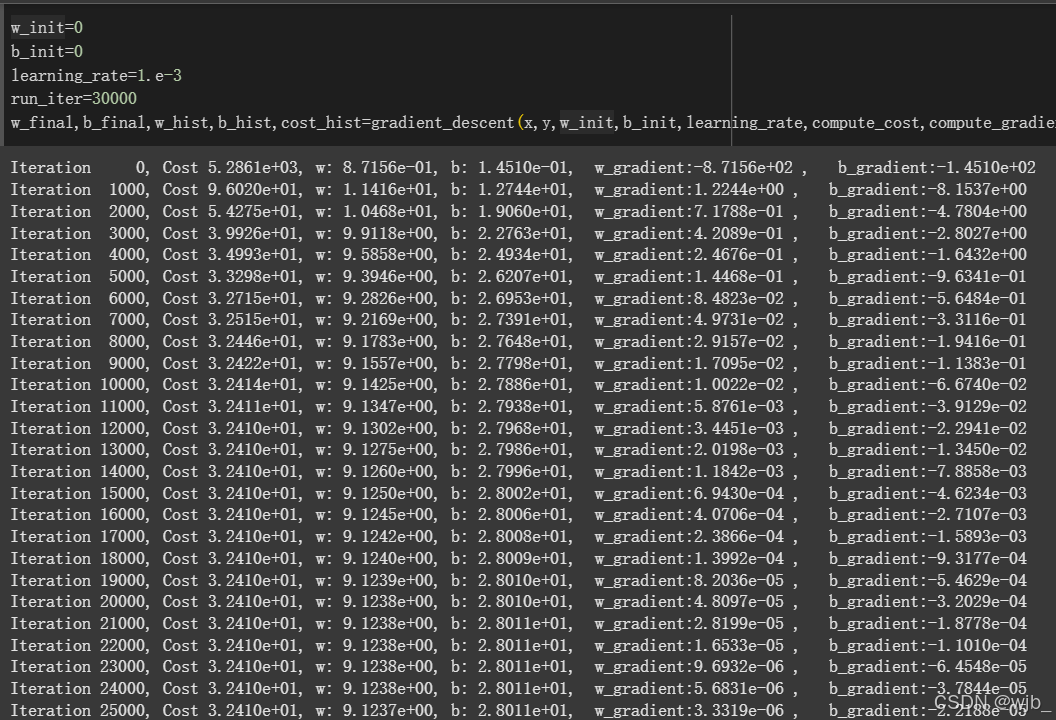
最终的w,b约为

员工年薪为3.5时,预测薪水应该给

可将cost与迭代的次数进行展示
import matplotlib.pyplot as plt
import numpy as np
plt.plot(np.arange(0,30000),cost_hist)
plt.title("itertion vs cost")
plt.xlabel("itertion")
plt.ylabel("cost")
plt.show()import matplotlib.pyplot as plt
import numpy as np
plt.plot(np.arange(0,100),cost_hist[:100])
plt.title("itertion vs cost")
plt.xlabel("itertion")
plt.ylabel("cost")
plt.show()下降的太快,可以查看前100次的情况
import matplotlib.pyplot as plt
import numpy as np
plt.plot(np.arange(0,100),cost_hist[:100])
plt.title("itertion vs cost")
plt.xlabel("itertion")
plt.ylabel("cost")
plt.show()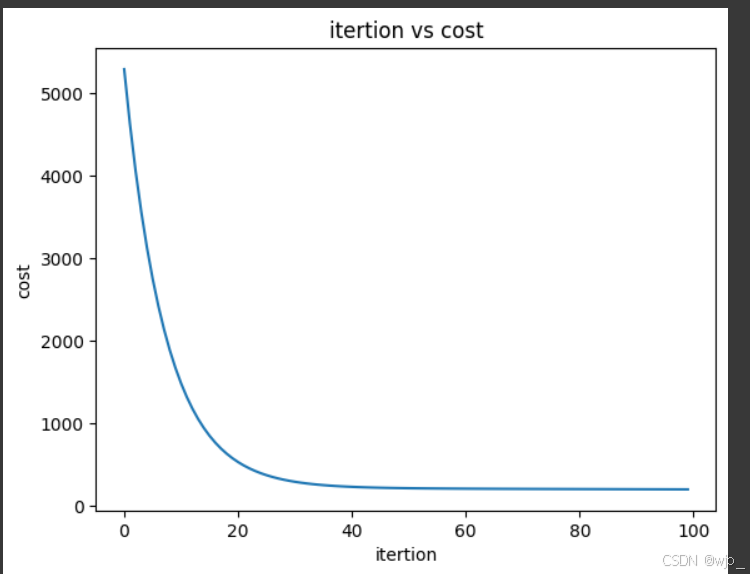
梯度下降过程的3D展示
w,b初试值为0,0的情况下
# w=-100~100 b=-100~100 的cost
import numpy as np
ws = np.arange(-100,101)
bs = np.arange(-100,101)
costs=np.zeros((201,201))i=0
for w in ws:j=0for b in bs:cost = compute_cost(x,y,w,b)costs[i,j]=costj=j+1i=i+1
costs!pip install wget
import wget
wget.download("https://github.com/GrandmaCan/ML/raw/main/Resgression/ChineseFont.ttf")from types import FrameType
import matplotlib as mlp
from matplotlib.font_manager import fontManager
fontManager.addfont("ChineseFont.ttf")
mlp.rc('font',family="ChineseFont")plt.figure(figsize=(7,7))
ax=plt.axes(projection="3d")
ax.view_init(45,-100) #第一参数是图像上下旋转,第二个是左右旋转
# ax.xaxis.set_pane_color((0,0,0))
# ax.yaxis.set_pane_color((0,0,0))
# ax.zaxis.set_pane_color((0,0,0))b_grid,w_grid= np.meshgrid(bs,ws)# cmap设置一个色彩
ax.plot_surface(w_grid,b_grid,costs,cmap="Spectral_r",alpha=0.2)
ax.set_title("w b 对应的cost")
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("cost")w_index,b_index=np.where(costs==np.min(costs))
print(f"当w={ws[w_index]},b={bs[b_index]} 会有最小cost:{costs[w_index,b_index]}")
ax.scatter(ws[w_index],bs[b_index],costs[w_index,b_index],color="red")ax.scatter(w_hist[0],b_hist[0],cost_hist[0],color="green")
ax.plot(w_hist,b_hist,cost_hist)
plt.show()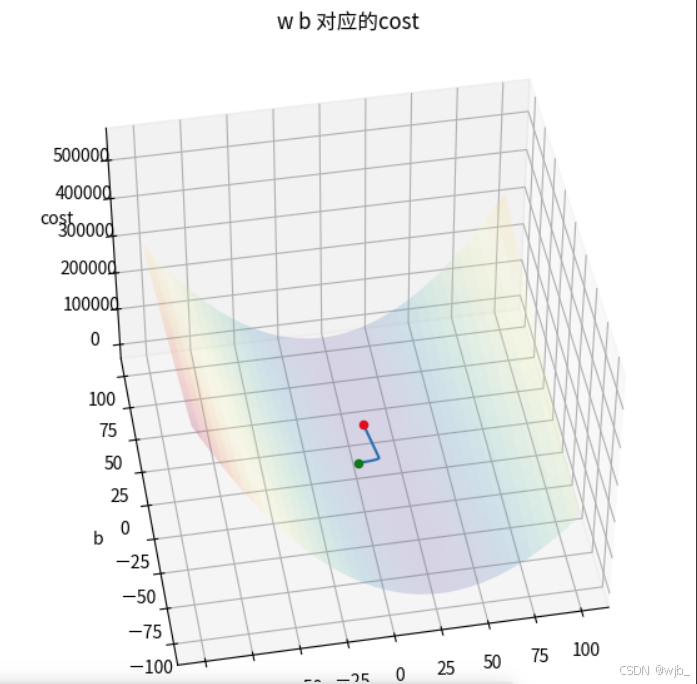
w,b初试值为-100 ,-100的情况下
w_init=-100
b_init=-100
learning_rate=1.e-3
run_iter=30000
w_final,b_final,w_hist,b_hist,cost_hist=gradient_descent(x,y,w_init,b_init,learning_rate,compute_cost,compute_gradient,run_iter)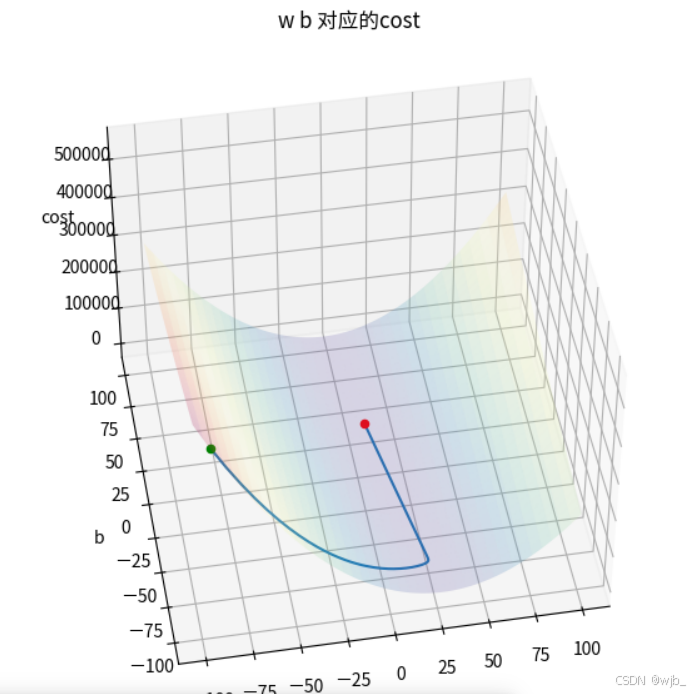
会发现,初始值并不是-100,-100 ,原因是代码中的初试点位是第一次更跟新后的结果
将运行次数改成100次
w_init=-100
b_init=-100
learning_rate=1.e-3
run_iter=100
w_final,b_final,w_hist,b_hist,cost_hist=gradient_descent(x,y,w_init,b_init,learning_rate,compute_cost,compute_gradient,run_iter)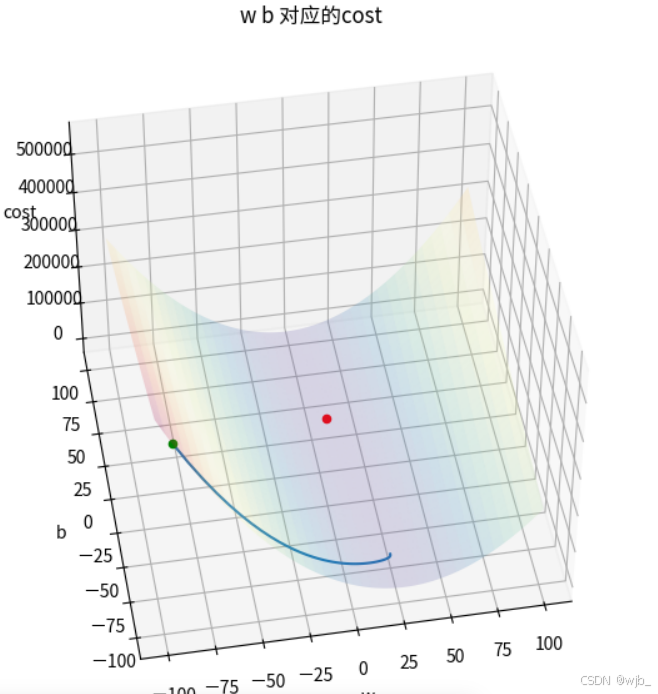
降低学率也会出现类似的效果
但是如果设置的特别大,我们可以想象到,他会过拟合,变成一条直线
若将学习率调整为1
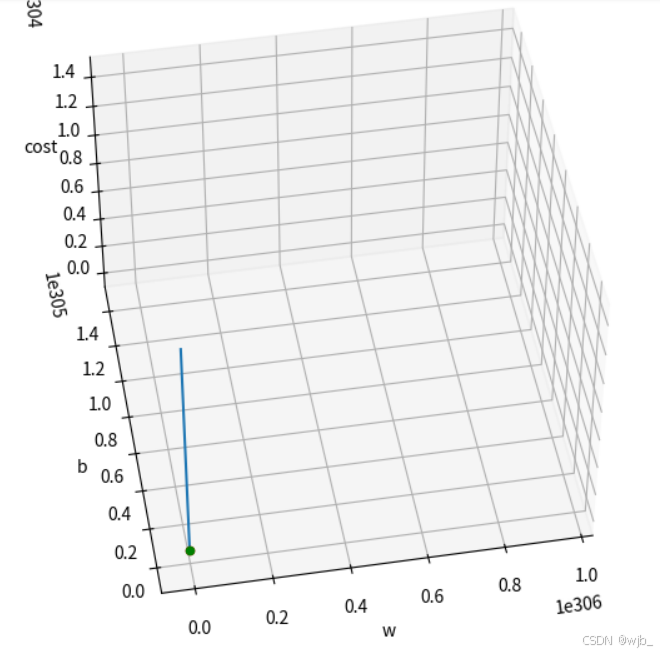
总结机器学习的过程
1.准备数据,根据数据分析应该采用什么样的模型进行表示,如本例中采用的是一条直线方程
2.紧接着找出最接近数据的具体模型,如本例中的比较拟合的一条直线
3.什么样的具体模型最拟合,需要给出评判的标准,本例中是设置的 点到直线距离平方的和
4.初始采用暴力枚举计算cost,后面为了提升效率,可以采用梯度下降算法
简单来说:
1.准备数据
2.设定模型
3.设定cost function
4.设定optimizer(优化器)
多元线性回归模型
在上面的例子中,如果只用之前的工资给出薪资,可能还不够,需要结合学历,地域,工作经验等 多个特征
one hot encoding
One-Hot Encoding(独热编码)是数据预处理中常用的一种技术,主要用于将分类数据转换为机器学习算法能够处理的数值数据。
基本概念
在很多机器学习任务中,模型通常只能处理数值型数据。但实际数据里常常包含分类变量,比如性别(男、女)、颜色(红、绿、蓝)等。One-Hot Encoding 的作用就是把这些分类变量转换为二进制向量表示。对于一个具有 个不同类别的分类变量,One-Hot Encoding 会创建 个新的二进制特征,每个特征对应一个类别。在这些特征中,只有一个特征的值为 1,表示该样本属于对应的类别,其余特征的值都为 0。
实现步骤
-
确定分类变量的所有可能取值:例如,对于 “颜色” 这个分类变量,可能的取值有 “红”、“绿”、“蓝”。
-
为每个取值创建一个新的特征:在上述例子中,会创建三个新特征,分别是 “颜色_红”、“颜色_绿”、“颜色_蓝”。
-
根据样本的实际取值,将对应的特征值设为 1,其余设为 0:如果一个样本的颜色是 “红”,那么 “颜色_红” 特征的值为 1,“颜色_绿” 和 “颜色_蓝” 特征的值为 0。
优缺点
优点
-
简单直观:易于理解和实现,能清晰地表示每个类别。
-
适用于大多数算法:很多机器学习算法都能很好地处理 One-Hot 编码后的数据。
-
保留类别信息:不会引入类别之间的顺序关系,因为每个类别都是独立的。
缺点
-
增加数据维度:当分类变量的类别数量较多时,会显著增加数据的维度,可能导致维度灾难,增加计算复杂度和存储需求。
-
可能导致稀疏矩阵:编码后的数据中大部分元素为 0,形成稀疏矩阵,对一些算法的性能有影响。
对于数据的维度问题,比如说男生,女生两个特征,合并为一个特征 是不是男生,对于一些情况,比如通过其中的几个特征,可推断出其他的特征,比如通过电话号码,可以知道姓名,性别,
住址等特征,都是降低维度的方法
载入数据
import pandas as pd
url="https://raw.githubusercontent.com/GrandmaCan/ML/main/Resgression/Salary_Data2.csv"
data=pd.read_csv(url)
data做映射(注意字符)
data["EducationLevel"]=data["EducationLevel"].map({"高中以下": 0, "大學": 1, "碩士以上": 2})
datask-learn
Scikit-learn(简称 sklearn)是一个用于机器学习的 Python 开源库,它提供了丰富的机器学习算法和工具,涵盖了分类、回归、聚类、降维等多种任务。
-
主要特点
-
简单易用:具有统一且简洁的 API 设计,使得用户可以轻松地调用各种机器学习算法进行建模和预测,即使是机器学习初学者也能快速上手。
-
丰富的算法:包含了众多经典和常用的机器学习算法,如线性回归、逻辑回归、决策树、随机森林、支持向量机、K 近邻算法、聚类算法(如 K-Means)等。
-
数据预处理工具:提供了各种数据预处理功能,例如数据标准化(StandardScaler)、归一化(MinMaxScaler)、特征选择(SelectKBest 等)等,帮助用户对原始数据进行清洗和转换,以适应模型的要求。
-
模型评估与选择:支持多种评估指标(如准确率、召回率、F1 值、均方误差等)和模型选择方法(如交叉验证),方便用户评估模型性能并选择最优的模型参数。
-
与其他库兼容:可以与 Python 的其他科学计算库(如 NumPy、pandas、Matplotlib 等)很好地集成和配合使用,便于数据处理、分析和可视化。
-
-
常见模块
-
sklearn.datasets:包含了一些常用的数据集,如鸢尾花数据集(load_iris)、手写数字数据集(load_digits)等,可用于快速测试和演示机器学习算法。
-
sklearn.preprocessing:提供数据预处理的类和函数,除了前面提到的标准化、归一化外,还有编码(如 LabelEncoder 用于将分类变量转换为数字编码)等功能。
-
sklearn.model_selection:主要用于模型的评估和选择,如 train_test_split 函数用于将数据集划分为训练集和测试集,GridSearchCV 用于通过网格搜索和交叉验证来寻找最优的模型参数。
-
sklearn.linear_model:实现了各种线性模型,如线性回归(LinearRegression)、逻辑回归(LogisticRegression)等。
-
sklearn.tree:包含决策树相关的类和函数,如 DecisionTreeClassifier 用于分类任务,DecisionTreeRegressor 用于回归任务。
-
sklearn.ensemble:集成学习模块,实现了随机森林(RandomForestClassifier、RandomForestRegressor)、梯度提升树(GradientBoostingClassifier、GradientBoostingRegressor)等集成算法。
-
sklearn.neighbors:实现了 K 近邻等基于邻居的算法,如 KNeighborsClassifier 用于分类,KNeighborsRegressor 用于回归。
-
-
使用示例
# 以使用 sklearn 进行简单的鸢尾花数据集分类为例from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建K近邻分类器对象,并设置邻居数为3
knn = KNeighborsClassifier(n_neighbors=3)# 训练模型
knn.fit(X_train, y_train)# 进行预测
y_pred = knn.predict(X_test)# 计算预测准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)对City one-hot-encoder A,B,C只需要知道两个就能知道下一个,可以降低维数
from sklearn.preprocessing import OneHotEncoder
onehot_encoder = OneHotEncoder()
onehot_encoder.fit(data[["City"]])
city_encoded =onehot_encoder.transform(data[["City"]]).toarray()
city_encodeddata[["CityA","CityB","CityC"]]=city_encoded
data=data.drop(["City","CityC"],axis=1)
data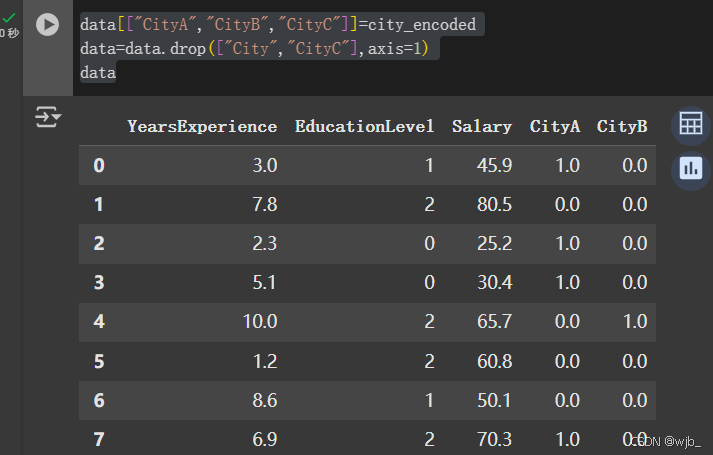
数据预处理
训练集,测试集 本例中设为8:2
from sklearn.model_selection import train_test_split
x=data[["YearsExperience","EducationLevel","CityA","CityB"]]
y=data["Salary"]
x_train, x_test, y_train,y_test=train_test_split(x,y,test_size=0.2)
x_train若不随机划分,可以改成
from sklearn.model_selection import train_test_split
x=data[["YearsExperience","EducationLevel","CityA","CityB"]]
y=data["Salary"]
x_train, x_test, y_train,y_test=train_test_split(x,y,test_size=0.2 , random_state=87)
x_train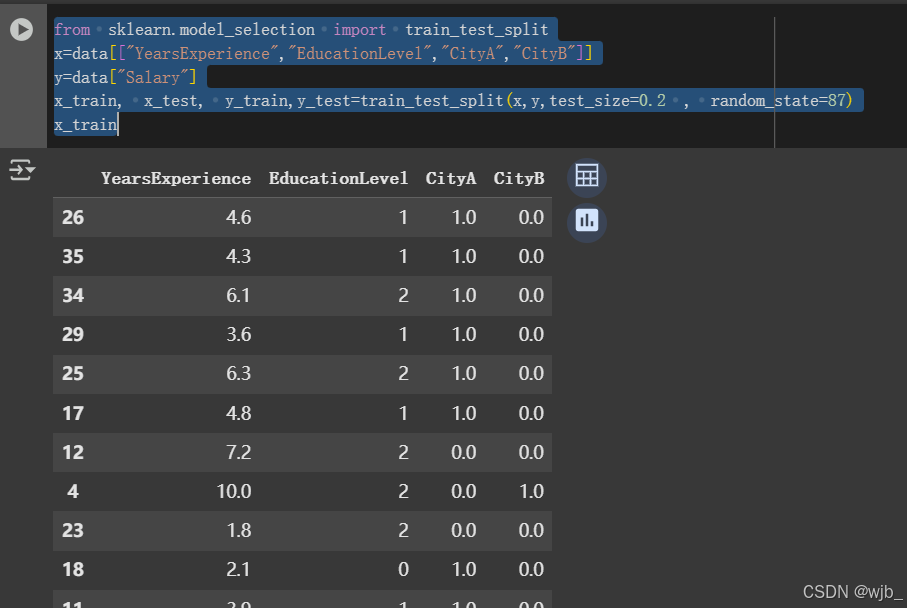
为了后续计算的方便,将pandas样式改成 numpy
x_train=x_train.to_numpy()
y_train=y_train.to_numpy()
x_train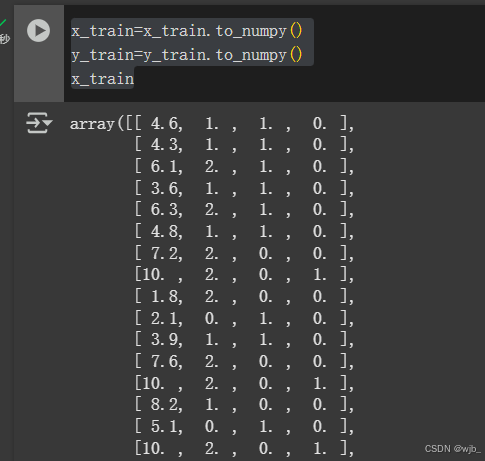
模型

