内容营销和传统营销的区别_博物馆展柜_淘宝关键词排名优化_黄山seo推广

目录​​​​​​​

1. 前言

2. Policy Gradient算法原理

2.1 公式原理

2.2 工作机制

3. Policy Gradient算法的优势

4. Policy Gradient算法的挑战

5. Policy Gradient算法：倒立摆稳定

6. 总结

---

1. 前言

在强化学习领域，Policy Gradient算法是一种直接优化策略的方法，与基于价值的方法不同，它不依赖于估计状态的价值函数。Policy Gradient算法通过调整策略的参数来最大化期望奖励，适用于处理连续动作空间和复杂任务。本文将详细介绍Policy Gradient算法的原理、优势、挑战，并提供一个完整的Python实现，帮助大家深入理解这一算法。

简单一句话就是：学习一种达到目标的策略，使得目标函数（每步奖励与决策概率对数函数的乘积之和）最大化。

2. Policy Gradient算法原理

2.1 公式原理

Policy Gradient算法的核心思想是通过计算目标函数J(θ)关于策略参数θ的梯度，来优化策略。目标函数J(θ)定义为：

其中，R_t是时间t的奖励，期望是基于策略πθ下的状态和动作分布，其中，τ 表示一个完整的轨迹（状态、动作、奖励的序列），πθ​ 是参数为 θ 的策略。

该式推导如下：

假设在一个episode中，智能体与环境交互所产生的状态信息和行为形成一个集合，称为迹。

对于某个迹而言，其发生的可能性可以表示为一系列条件概率的乘积。

其中，θ是智能体决策参数，可以当做智能体自己的神经网络中的权重。

用连乘符号，上面这个式子可以表示为：

对于某智能体而言，在多个episode中，得到的迹可能是不同的。因此，训练智能体的最终目标是要最大化在各个迹上的期望奖励。

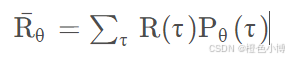
又可以表示为：

为了最大化 J(θ)，我们计算其梯度： 

其中：

• logπθ​(at​∣st​) 是动作 at​ 在状态 st​ 下的对数概率。

• R(τ) 是轨迹 τ 的累积奖励。

2.2 工作机制

1. Rollout：代理按照当前策略与环境交互，收集状态、动作和奖励。

2. 计算回报：计算从时间t开始的累积奖励G_t，通常使用折扣和的方式。

3. 计算梯度：使用收集的数据计算目标函数关于策略参数的梯度。

4. 更新策略：通过梯度上升更新策略参数，以提高期望回报。

3. Policy Gradient算法的优势

1. 处理连续动作空间：Policy Gradient算法能够处理连续和高维的动作空间，而传统的基于价值的方法则难以做到。

2. 直接优化策略：无需近似价值函数，直接优化策略。

3. 复杂环境表现良好：在具有复杂状态空间和难以估计价值函数的环境中表现良好。

4. Policy Gradient算法的挑战

1. 高方差：策略梯度估计通常具有高方差，导致训练不稳定。可以通过使用基线函数或PPO等方法来降低方差。

2. 样本效率低：需要大量与环境的交互才能收敛。

3. 局部最优：可能陷入局部最优，导致策略次优。

5. Policy Gradient算法：倒立摆稳定

以下是一个使用Policy Gradient算法解决CartPole问题的Python实现：

import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical
from collections import deque# 改进后的策略网络
class Policy(nn.Module):def __init__(self):super(Policy, self).__init__()self.fc1 = nn.Linear(4, 128)  # 输入层self.fc2 = nn.Linear(128, 128)  # 隐藏层self.fc3 = nn.Linear(128, 2)  # 输出层self.saved_log_probs = []self.rewards = []self.entropy = []  # 用于熵正则化def forward(self, x):x = torch.relu(self.fc1(x))x = torch.relu(self.fc2(x))x = self.fc3(x)return xdef act(self, state):state = torch.from_numpy(state).float().unsqueeze(0)logits = self.forward(state)probs = torch.softmax(logits, dim=-1)m = Categorical(probs)action = m.sample()# 记录熵正则化项（确保是1维张量）entropy = m.entropy().mean().unsqueeze(0)self.entropy.append(entropy)self.saved_log_probs.append(m.log_prob(action))return action.item()# 训练函数
def reinforce_with_baseline(n_episodes=1000, max_t=1000, gamma=0.99,print_every=100, entropy_coeff=0.01):scores_deque = deque(maxlen=100)scores = []policy = Policy()optimizer = optim.Adam(policy.parameters(), lr=3e-4)  # 调整学习率for i_episode in range(1, n_episodes + 1):saved_log_probs = []rewards = []entropy = []state, _ = env.reset()for t in range(max_t):action = policy.act(state)saved_log_probs.append(policy.saved_log_probs[-1])entropy.append(policy.entropy[-1])state, reward, done, _, _ = env.step(action)rewards.append(reward)if done:break# 计算折扣奖励R = 0returns = []for r in reversed(rewards):R = r + gamma * Rreturns.insert(0, R)# 归一化奖励returns = torch.tensor(returns)returns = (returns - returns.mean()) / (returns.std() + 1e-8)# 计算策略损失policy_loss = []for log_prob, R in zip(saved_log_probs, returns):policy_loss.append(-log_prob * R)# 添加熵正则化entropy_loss = -torch.cat(entropy).mean() * entropy_coeff# 总损失loss = torch.cat(policy_loss).sum() + entropy_loss# 更新策略网络optimizer.zero_grad()loss.backward()optimizer.step()# 记录分数scores_deque.append(sum(rewards))scores.append(sum(rewards))if i_episode % print_every == 0:print('Episode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_deque)))return scores, policy# 初始化环境
env = gym.make('CartPole-v1')# 训练改进后的策略
scores, policy = reinforce_with_baseline(n_episodes=1000, entropy_coeff=0.01)# 测试策略
def test_policy(policy, env, n_episodes=100):scores = []for _ in range(n_episodes):state, _ = env.reset()score = 0while True:action = policy.act(state)state, reward, done, _, _ = env.step(action)score += rewardif done:breakscores.append(score)return np.mean(scores)# 测试并打印结果
avg_score = test_policy(policy, env, n_episodes=100)
print(f'Average Score over 100 episodes: {avg_score:.2f}')

• Categorical(probs) 定义一个分类分布（Categorical Distribution），其中 probs 是动作的概率分布。

• 这个分布用于从动作空间中采样动作。

• m.log_prob(action) 计算采样动作的对数概率。

• self.saved_log_probs 是一个列表，用于保存每个采样动作的对数概率。

• 这些对数概率在后续计算策略梯度时会用到。

• n_episodes：训练的总回合数，默认为1000。每个回合代表与环境的一次完整交互，直到环境终止。

• max_t：每个回合的最大时间步数，默认为1000。用于限制每个回合的长度，防止无限循环。

• gamma：奖励的折扣因子，默认为0.99。用于计算累积奖励时的折扣，强调近期奖励或远期奖励的重要性。

• print_every：打印信息的间隔，默认为100。每print_every个回合打印一次当前的平均奖励，用于监控训练进度。

熵正则化的效果

• 探索性增强：熵正则化鼓励策略在训练过程中尝试更多的动作，避免过早收敛到局部最优解。

• 稳定性提升：通过增加探索，策略能够更好地适应环境的变化，提高训练的稳定性。

• 超参数调整：entropy_coeff 控制熵损失的权重。较大的值会增加探索，但可能导致收敛速度变慢；较小的值可能减少探索，但可能导致局部最优。

6. 总结

Policy Gradient算法是一种强大的强化学习方法，适用于处理连续动作空间和复杂任务。通过直接优化策略，它能够有效地解决传统基于价值的方法难以处理的问题。然而，该算法也面临高方差和样本效率低等挑战。通过使用基线函数或更先进的方法（如PPO），可以有效降低方差并提高训练稳定性。本文提供的Python实现展示了如何使用Policy Gradient算法解决CartPole问题，为大家提供了一个直观的学习和实践示例。我是橙色小博，关注我，一起在人工智能领域学习进步！