题意
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
提示:
-
1 <= nums.length <= 6
-
-10 <= nums[i] <= 10
-
nums中的所有整数 互不相同
难度
中等
示例
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
分析
题意非常朴素,让我们找出nums的所有排列组合。
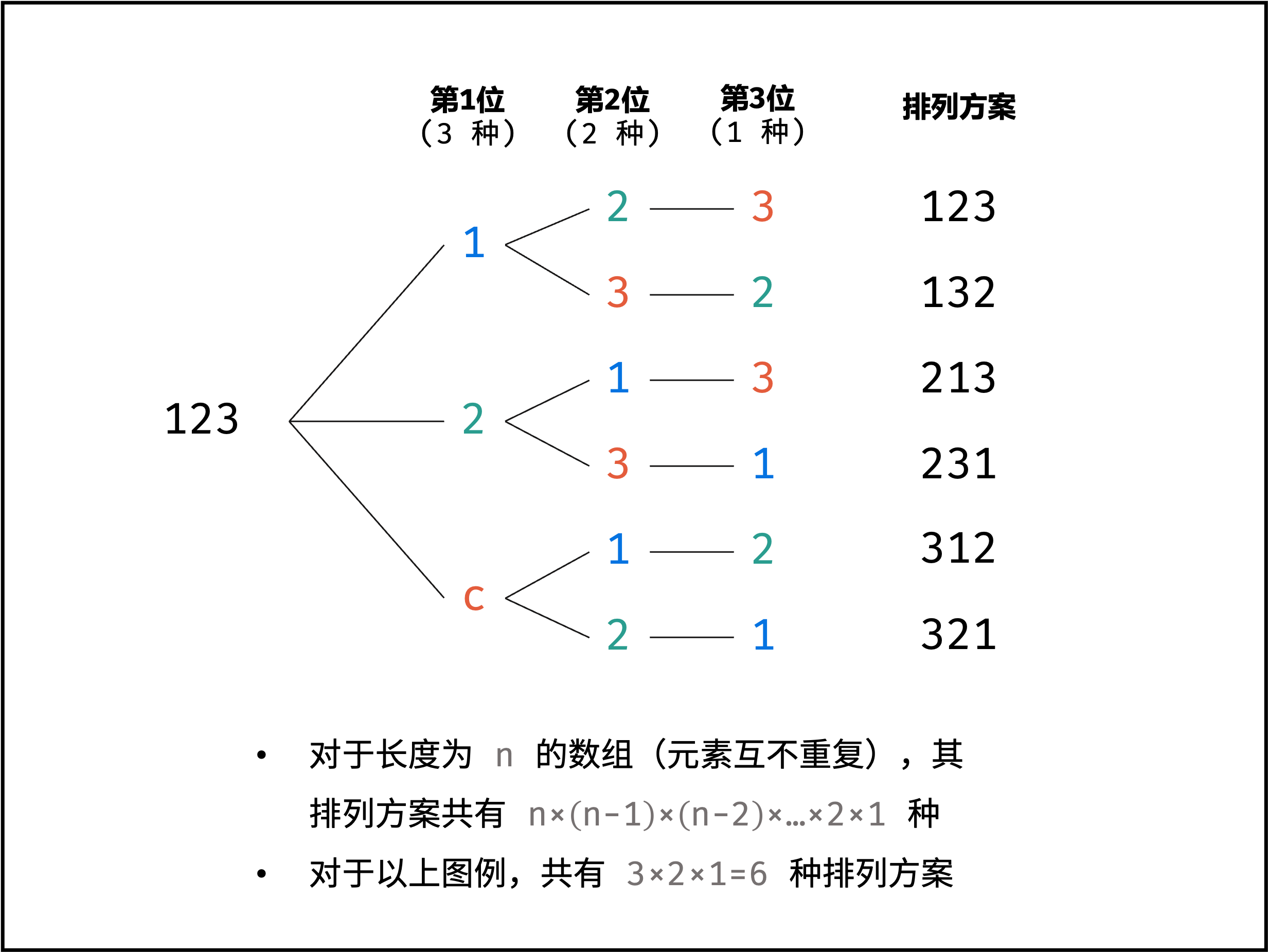
总数:是一个n的阶乘。
那我们就可以用回溯算法来解决,遍历数组的每一个元素,然后尝试生成所有的排列,当生成一个完整的排列时,记录该排列,并退回到上一步,然后继续生成新的排列。
就比如说“123”,我们可以先固定 1,然后递归处理 “23”。把 “123”、“132” 排列完成后,回溯到上一步,固定 2,然后递归处理 “13”,以此类推。
public class Main04601 {public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();boolean[] used = new boolean[nums.length]; // 标记数字是否被使用backtrack(nums, result, path, used);return result;}// 回溯算法private void backtrack(int[] nums, List<List<Integer>> result, List<Integer> path, boolean[] used) {// 如果当前排列的长度等于 nums 的长度,则找到一个完整的排列if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 将当前排列加入结果列表return;}// 遍历每一个数字,尝试将其加入排列for (int i = 0; i < nums.length; i++) {// 如果该数字已经使用过,则跳过if (used[i]) {continue;}// 做选择:选择当前数字path.add(nums[i]);used[i] = true;// 继续递归处理剩余数字的排列backtrack(nums, result, path, used);// 撤销选择:回溯path.remove(path.size() - 1);used[i] = false;}}public static void main(String[] args) {Main04601 solution = new Main04601();int[] nums = {1, 2, 3};List<List<Integer>> result = solution.permute(nums);System.out.println(result); // 输出所有全排列}
}简单解释一下。
①、主方法 permute 中:
-
初始化结果列表 result,用于存储所有可能的排列。
-
初始化路径列表 path,用于记录当前的排列。
-
使用布尔数组 used 标记某个数字是否被使用。
-
调用回溯算法 backtrack,开始生成排列。
②、回溯算法 backtrack 中:
-
如果当前排列的长度等于 nums 的长度,则找到一个完整的排列,将其加入结果列表。
-
遍历 nums 中的每一个数字,尝试将其加入排列。
-
如果该数字已经使用过,则跳过。
-
做选择:选择当前数字,将其加入排列,并标记为已使用。
-
继续递归处理剩余数字的排列。
-
撤销选择:回溯,将当前数字从排列中移除,并标记为未使用。

主要看 path 在整个递归过程中的变化。整个题解的效率还不错。

总结
回溯算法非常适合这种全排列的题目,无非就是做选择、递归、撤销选择。
力扣链接:. - 力扣(LeetCode)
