目录
- 一、 Vector set as 输入
- 二、 模型输出(三种)
- 1 **n-to-n**
- 2 n-to-1
- 3 n-to-m
- 三、self-attention
- 1、问题引入
- 2、self-attention
- 3 self-attention 原理介绍
一、 Vector set as 输入
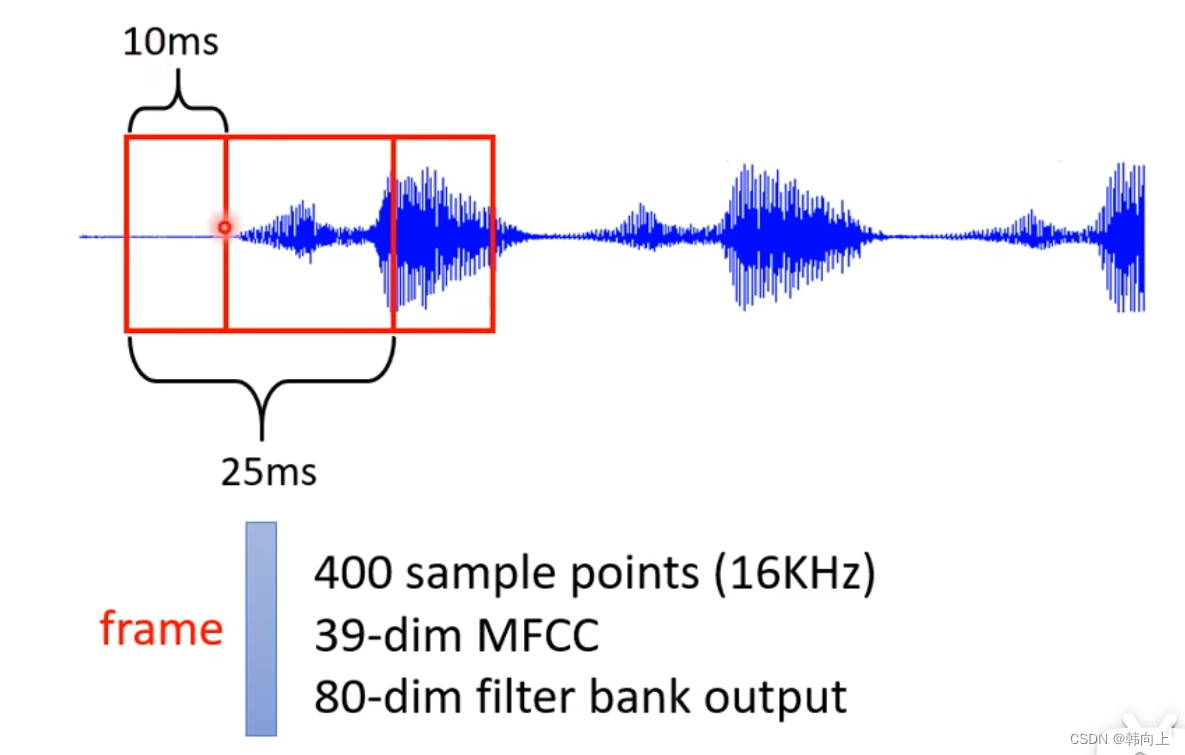
一段声音讯号:
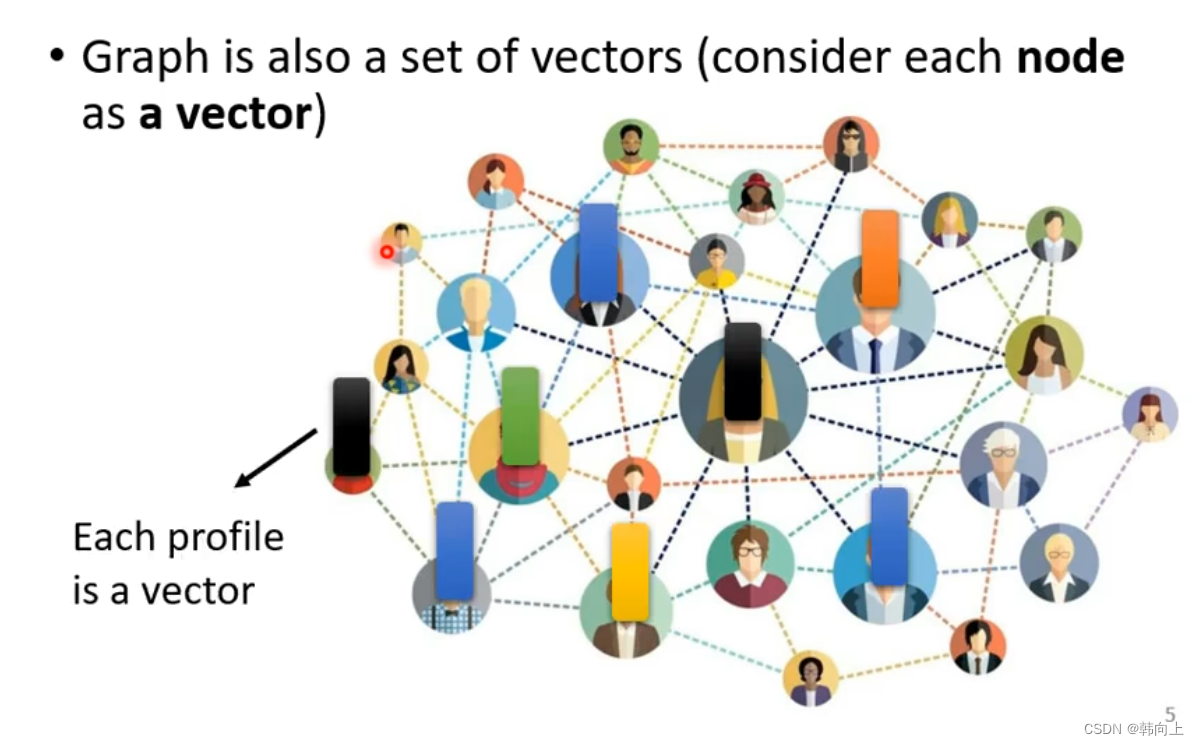
图结构(graph):输入向量(vector={性别,身高})
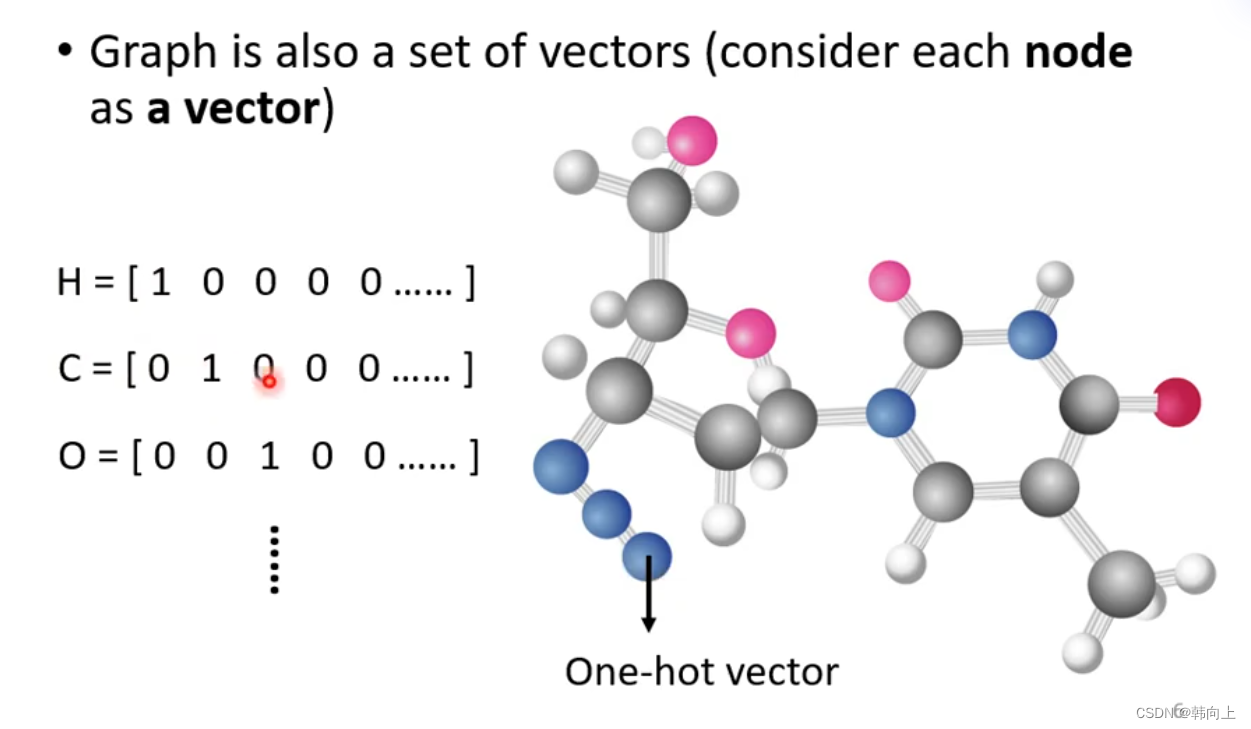
分子结构:vector={元素类别}
二、 模型输出(三种)
1 n-to-n
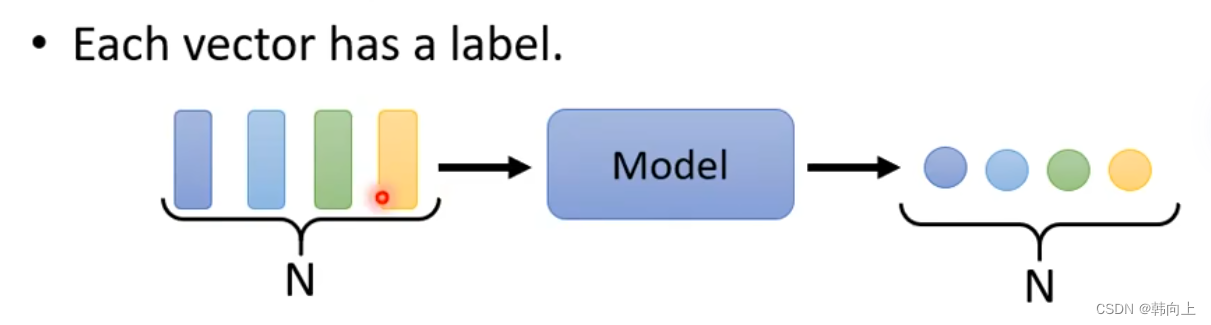
应用:文字处理
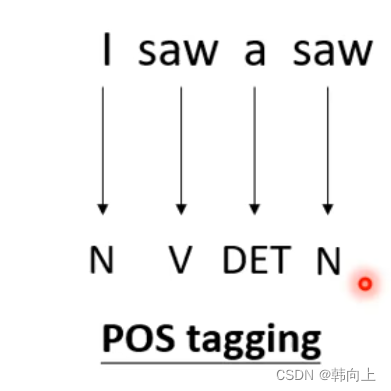
语音识别:
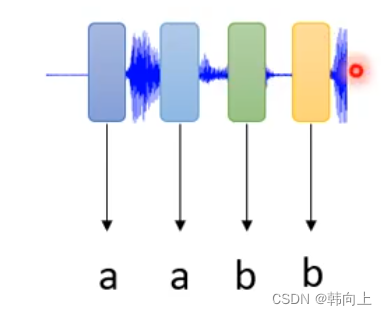
2 n-to-1
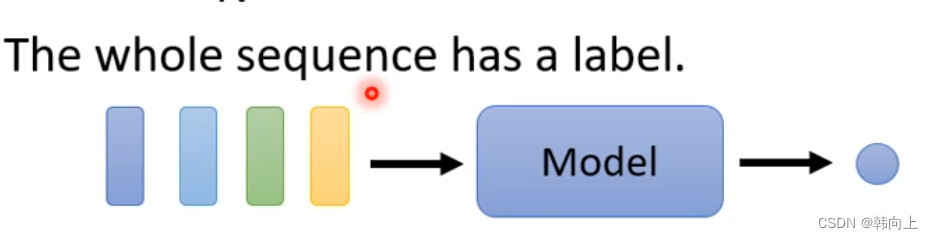
应用:正负评论分类、语音辨认
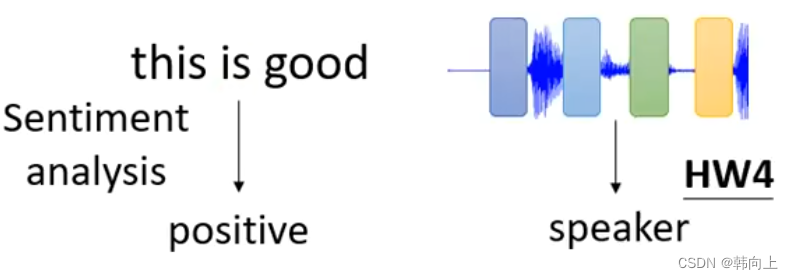
3 n-to-m
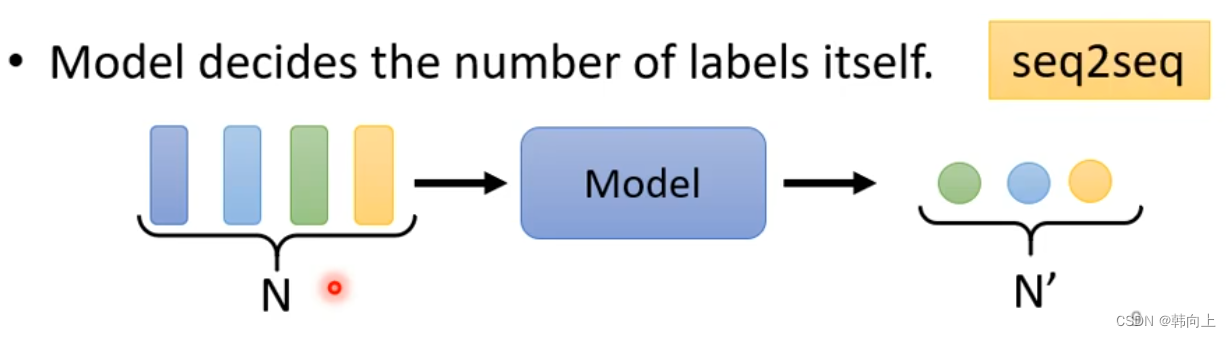
应用:翻译
三、self-attention
以n-to-n为例。
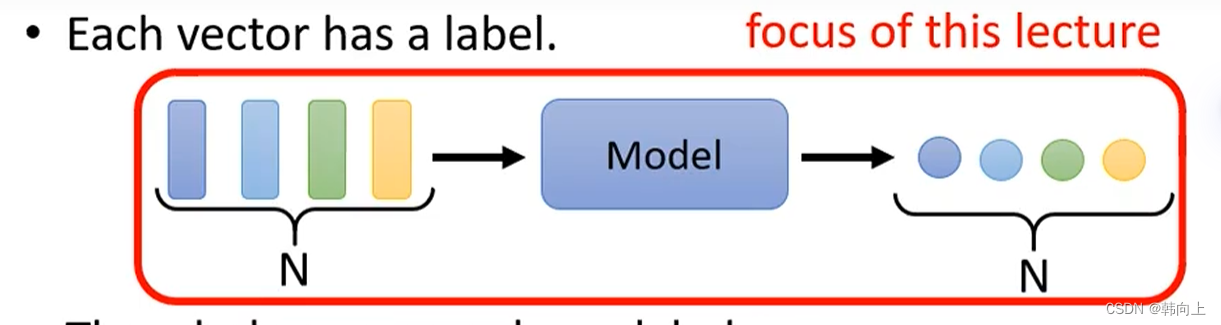
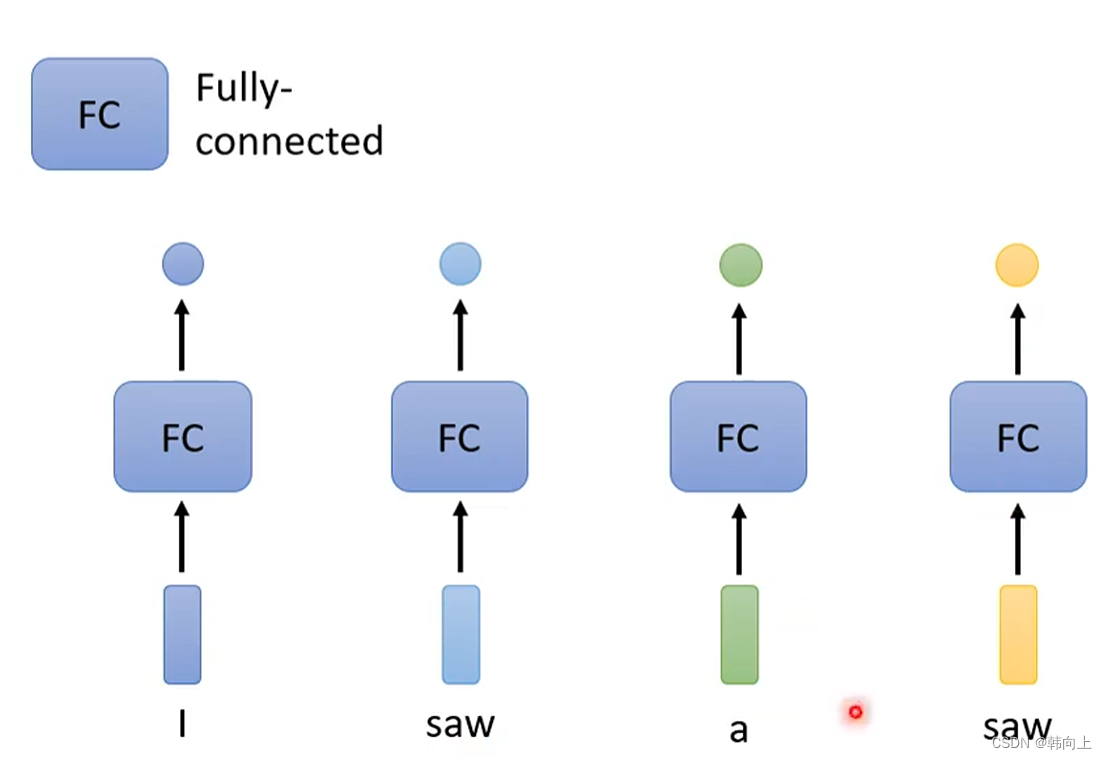
1、问题引入
不考虑上下文的情况下,模型认为两个"saw"是一样的,会输出相同的两个结果。
使用Window局部考虑上下文:
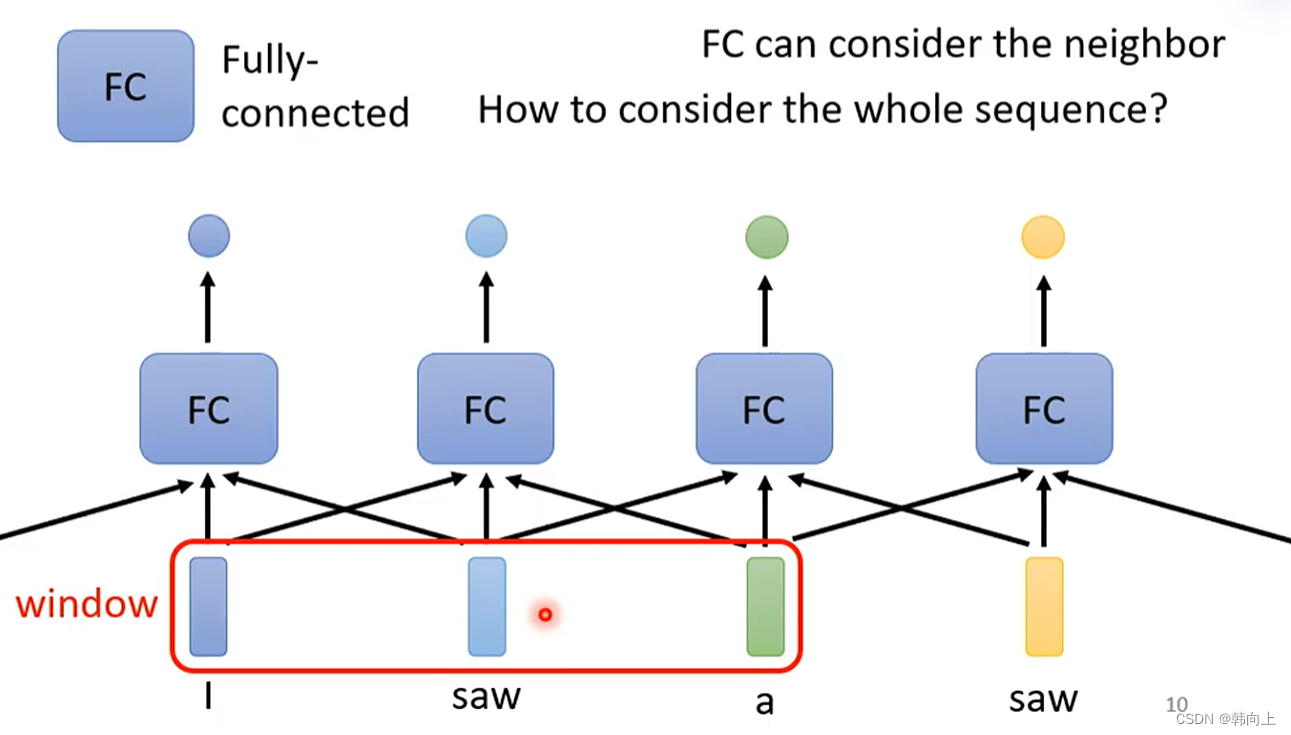
使用Windows考虑上下文,无法考虑整个序列的上下,如果想要考虑较长的上下文信息,需要大的Window,这样就增加计算复杂度。
————————————————————————————————————————
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
————————————————————————————————————————
2、self-attention
Transformer是一个经典的self-attention 论文,
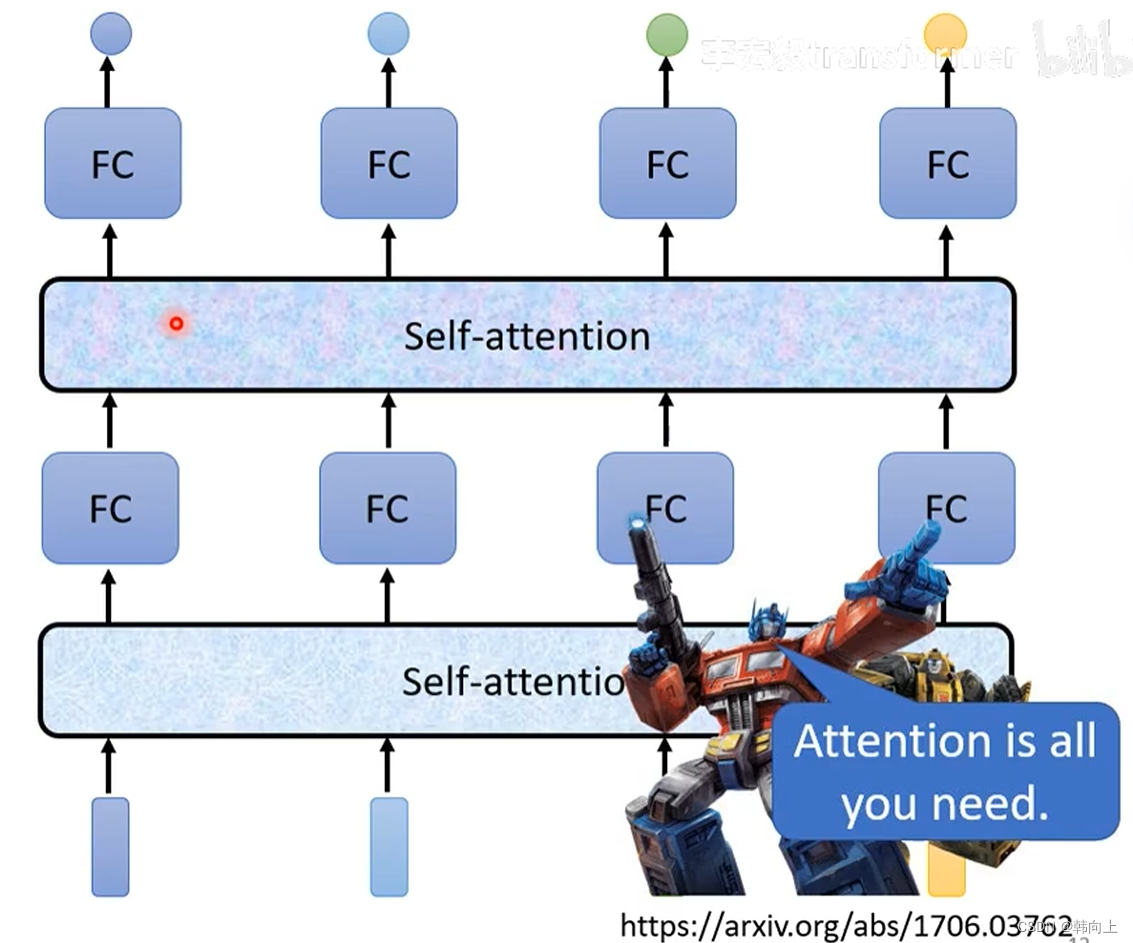
3 self-attention 原理介绍
找出任意两个输入的相关性 α \alpha α:
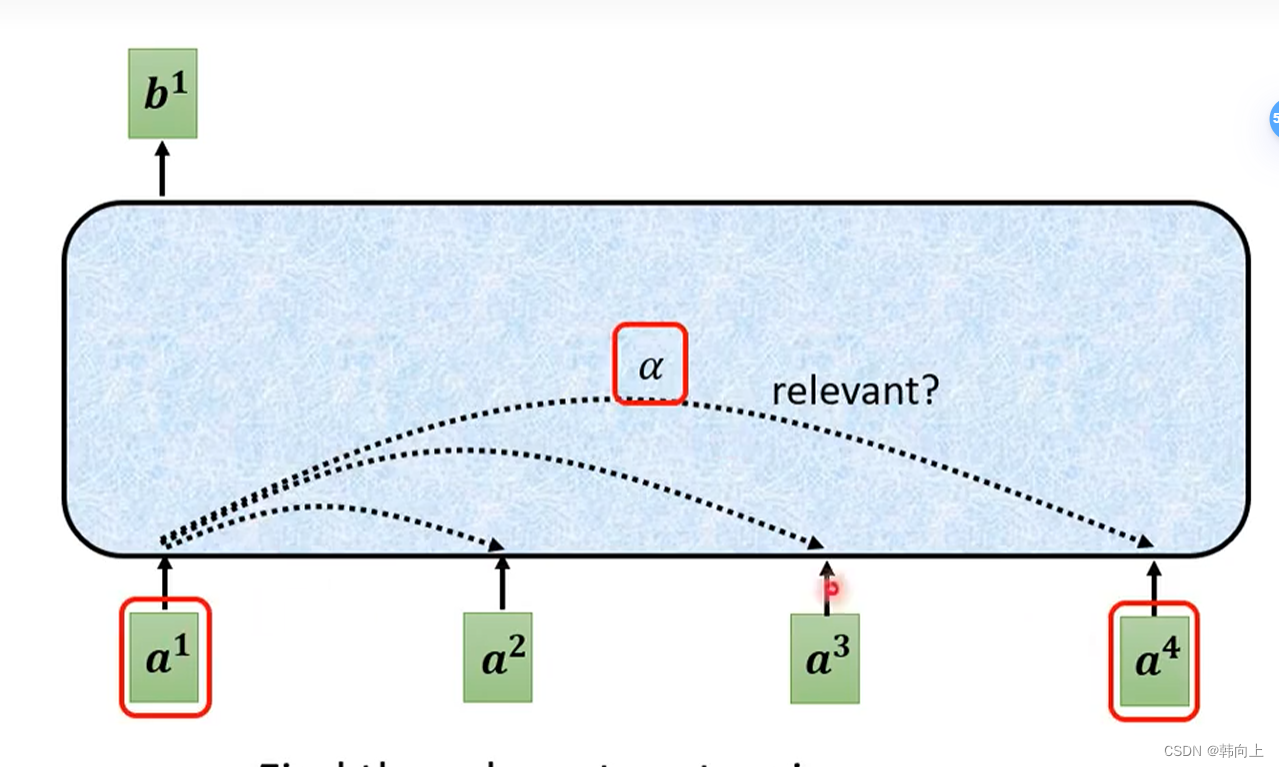
计算 α \alpha α(两种方式:1 dot product, 2 additive):
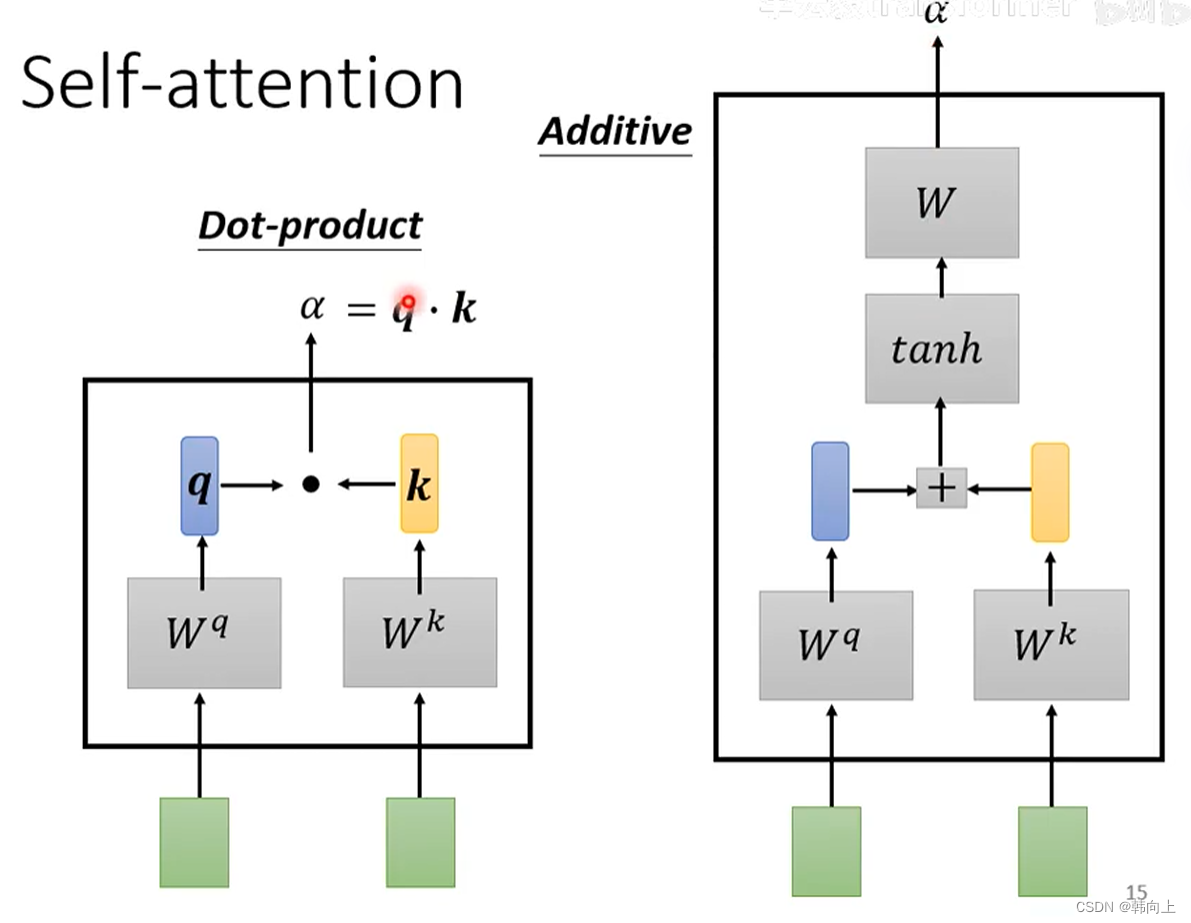
有了 α \alpha α的计算方式,接下来计算输入之间的关联性:
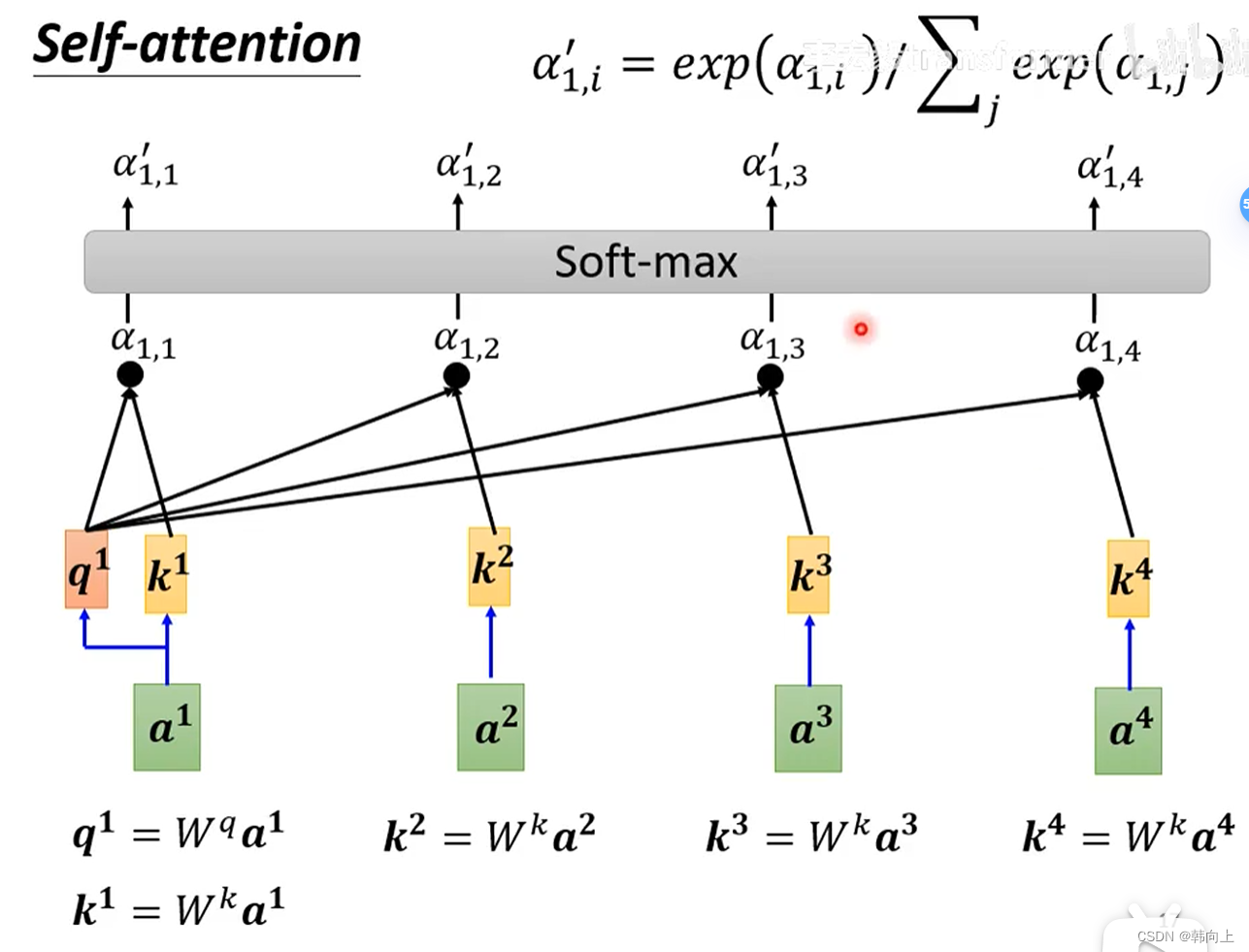
获得 a 1 a_1 a1与其他输入向量的相关性: α 1 = [ α 1 , 1 ′ α 1 , 2 ′ α 1 , 3 ′ α 1 , 4 ′ ] \alpha_1=[\alpha' _{1,1} \alpha' _{1,2} \alpha' _{1,3} \alpha' _{1,4}] α1=[α1,1′α1,2′α1,3′α1,4′],接下来利用关系向量作为权重乘上输入向量 [ a 1 , a 2 , a 3 , a 4 ] [a^1,a^2,a^3,a^4] [a1,a2,a3,a4],得到考虑上下文的 a 1 a^1 a1,即 b 1 b^1 b1:
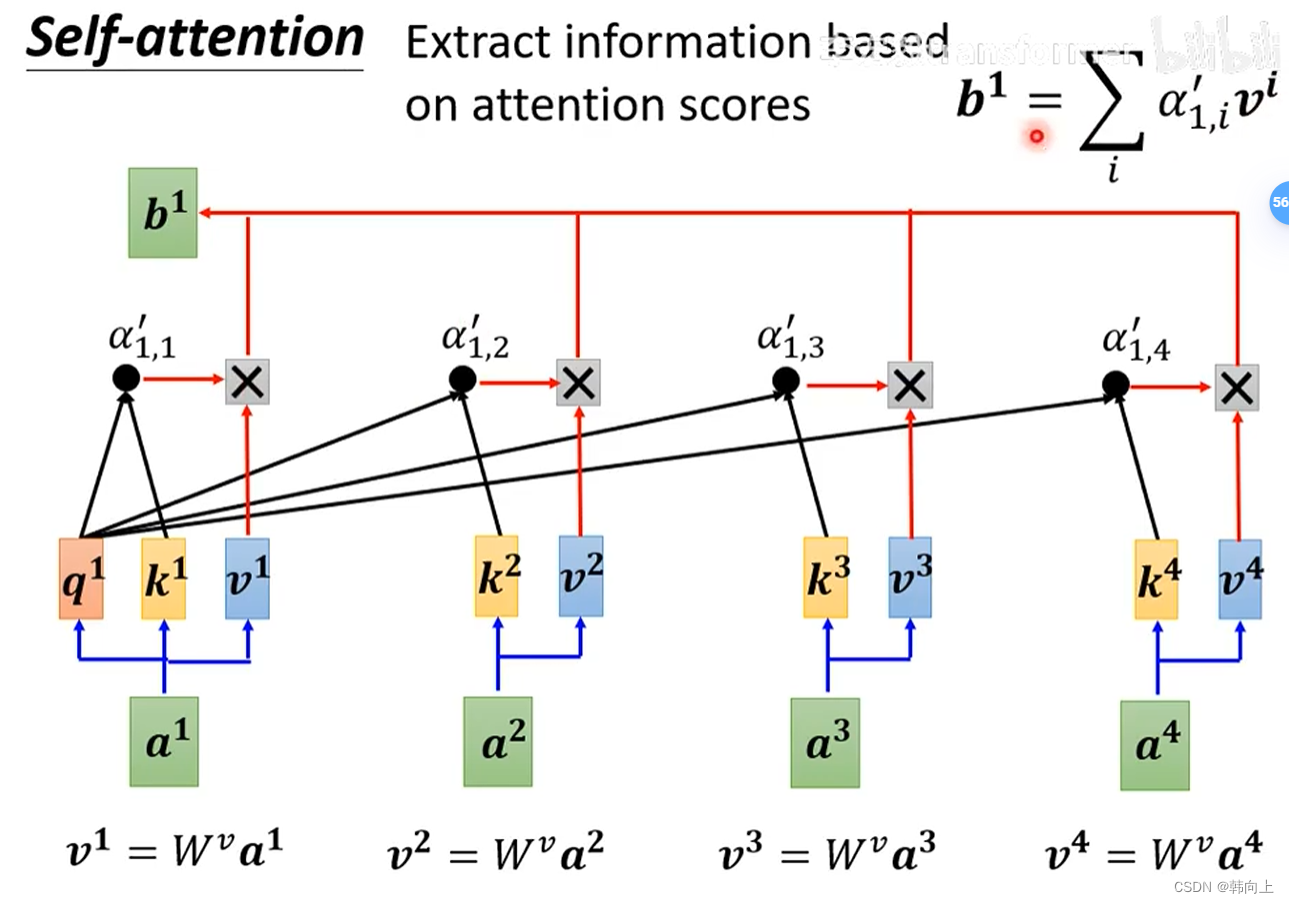
接下来,就能计算 [ b 1 , b 2 , b 3 , b 4 ] [b^1,b^2,b^3,b^4] [b1,b2,b3,b4]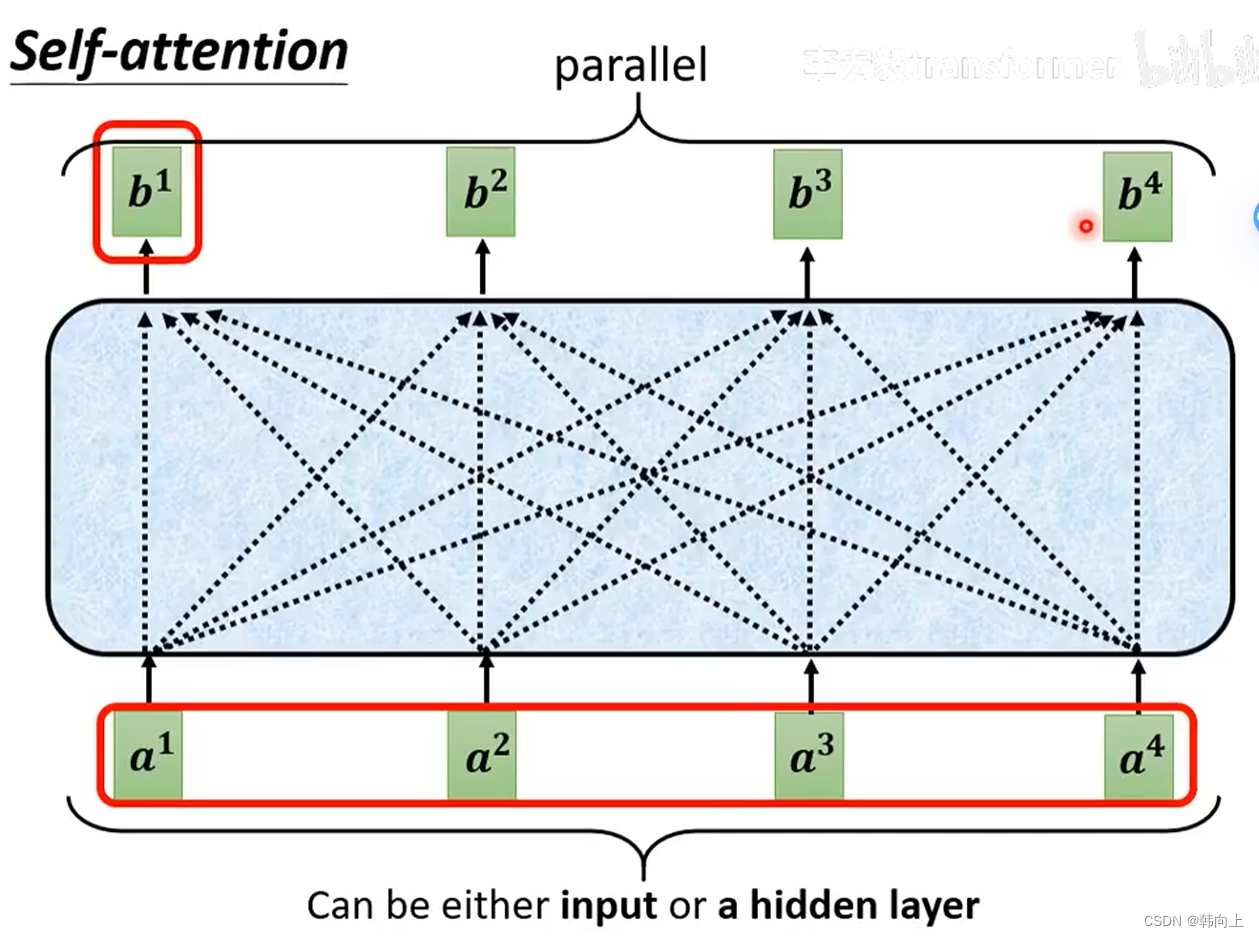
[ b 1 , b 2 , b 3 , b 4 ] [b^1,b^2,b^3,b^4] [b1,b2,b3,b4]并不是串行计算,而是通过矩阵乘法进行并行计算:
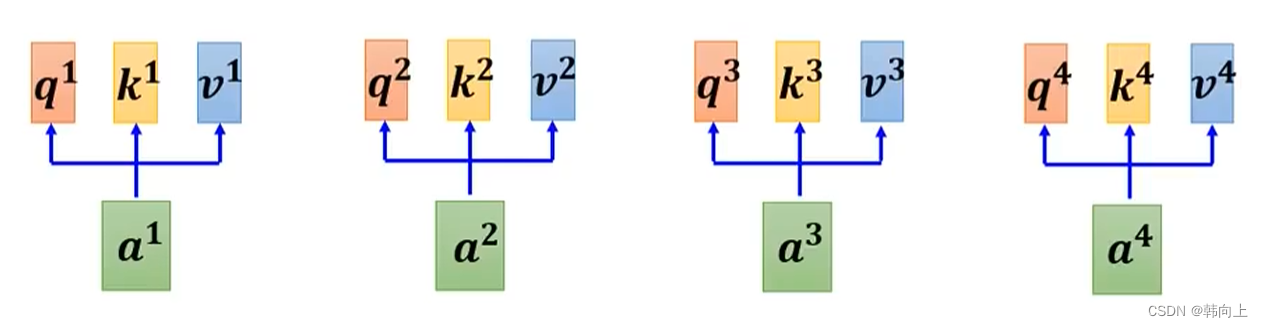
对于 [ q 1 , q 2 , q 3 , q 4 ] [q^1,q^2,q^3,q^4] [q1,q2,q3,q4], K 1 , k 2 , k 3 , k 4 K^1,k^2,k^3,k^4 K1,k2,k3,k4, v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4,可以通过矩阵乘法实现并行计算:
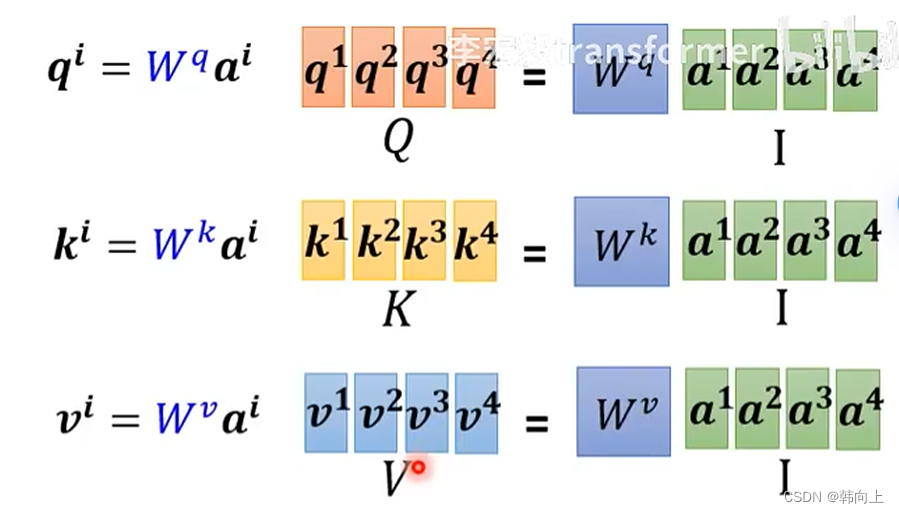
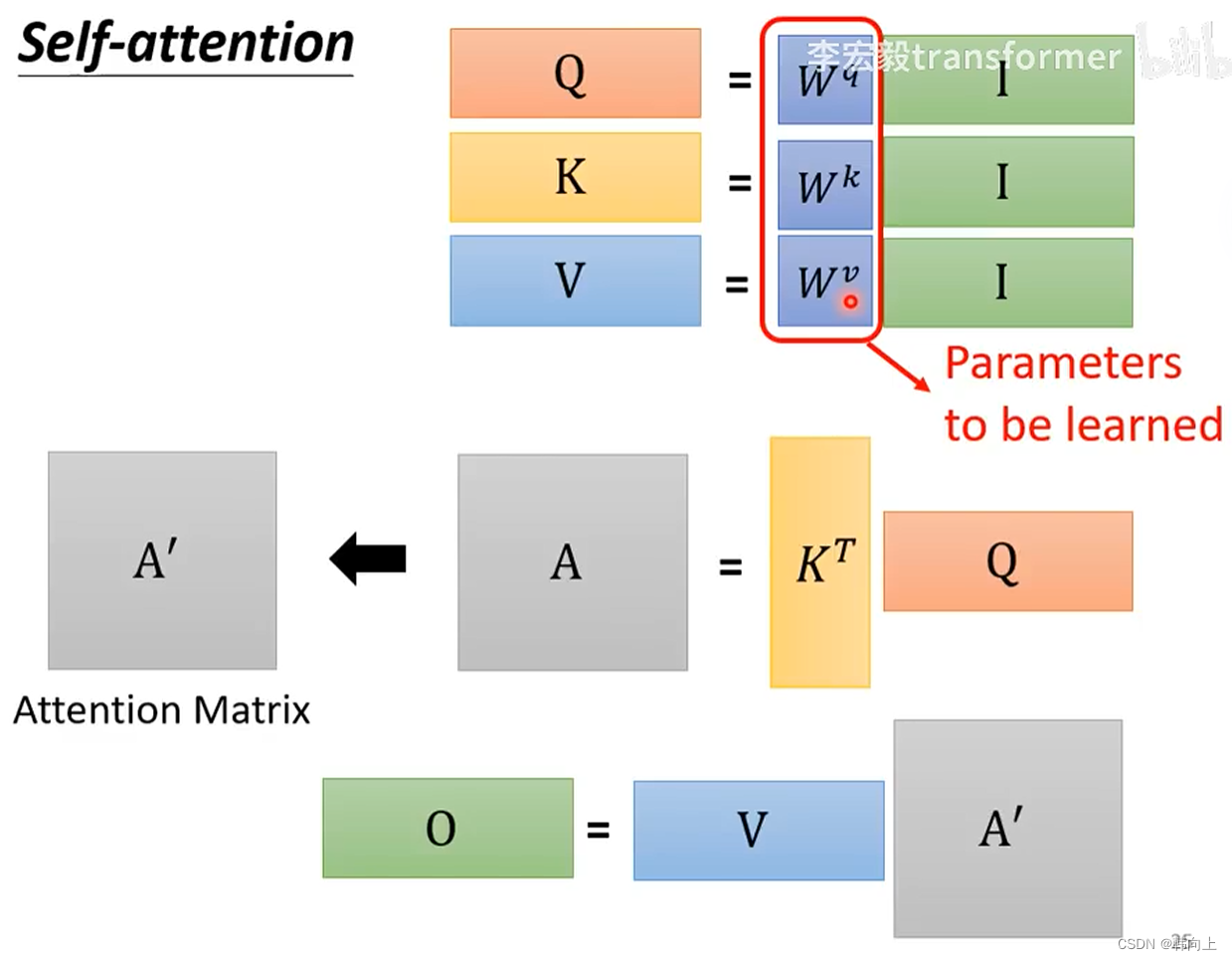
接下来我们就可以使用得到的Q,K,V计算相关性系数 α \alpha α。同样也可以使用矩阵乘法来实现并行计算,即 K T ∗ Q K^T*Q KT∗Q:
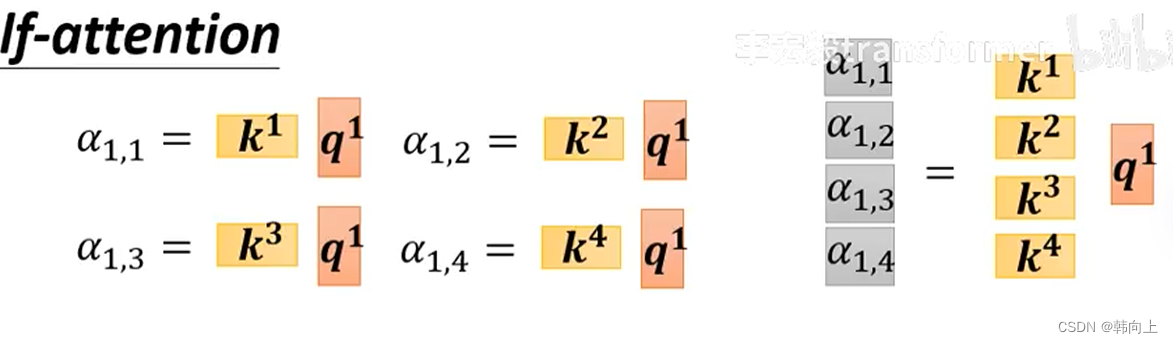
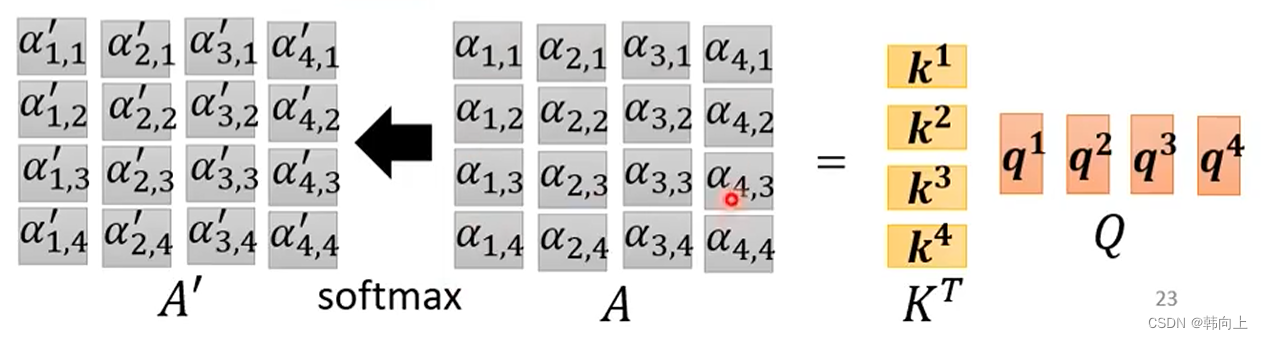
得到相关性矩阵 A A A之后,就可以计算考虑上下文的特征向量 b b b。
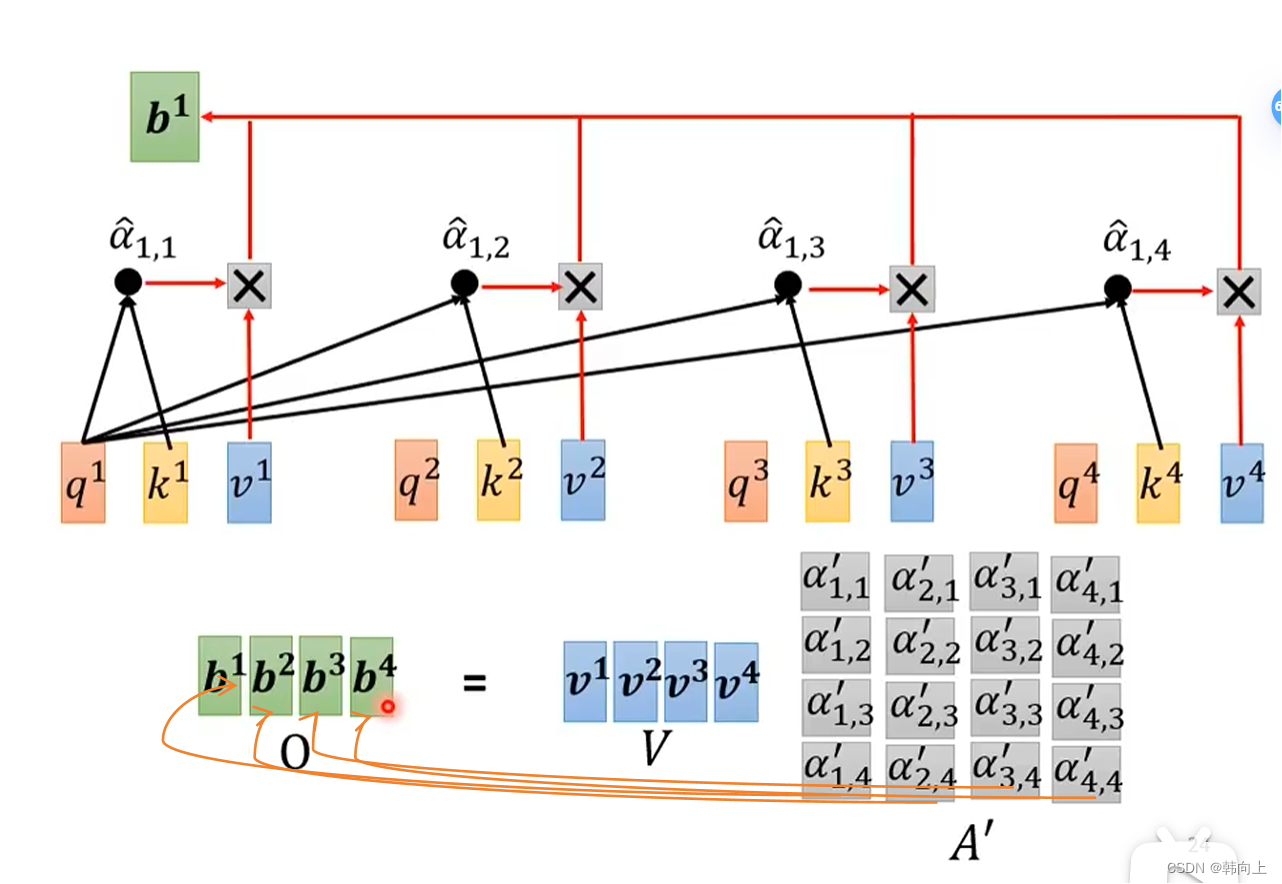
所以self-attention的计算过程被总结为如下的矩阵乘法: