前言
本篇博客我们来看一些二叉树的经典题型,也是对上篇博客的补充
💓 个人主页:小张同学zkf
⏩ 文章专栏:数据结构
若有问题 评论区见📝
🎉欢迎大家点赞👍收藏⭐文章


目录
1.单值二叉树
2.检查两棵树是否相同
3.对称二叉树
编辑
4.二叉树的前序遍历
5.另一棵树的子树
1.单值二叉树

这道题有两种思路,一种是最简单的也是最常见的思路,遍历,就是把每个节点遍历一遍,看是否值相等(代码过于简单就不写了),还有一种思路就是递归,通过递归,判断孩子与父亲是否相等,若相等进行下次递归,直到节点为空,就代表是单值二叉树,我们写下递归方式的代码
代码如下

2.检查两棵树是否相同
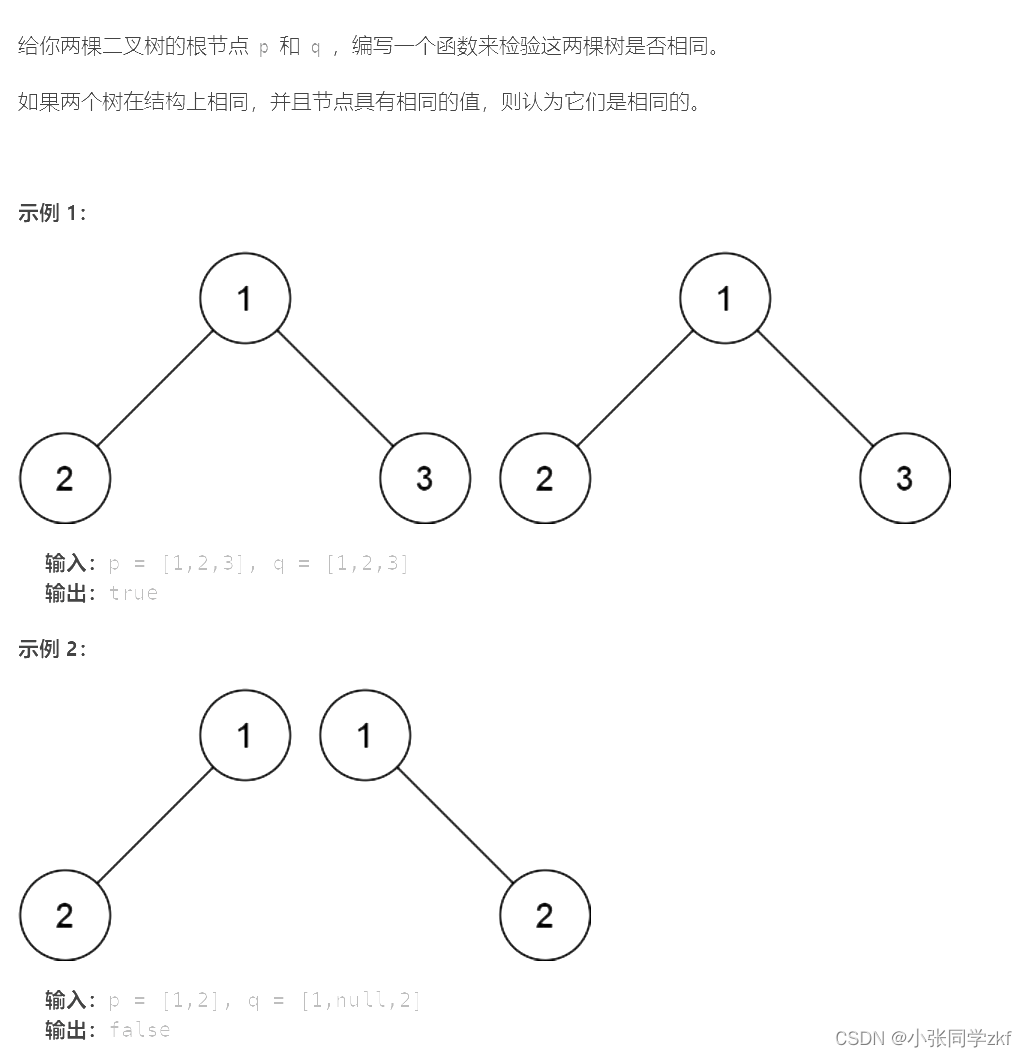
这道题我们可以让两颗子树分别遍历,直到双方节点同时都为空,就相等若是一方节点先为空则两棵树不相等,若遍历的同时值不相等,那两棵树也不相等,代码如下

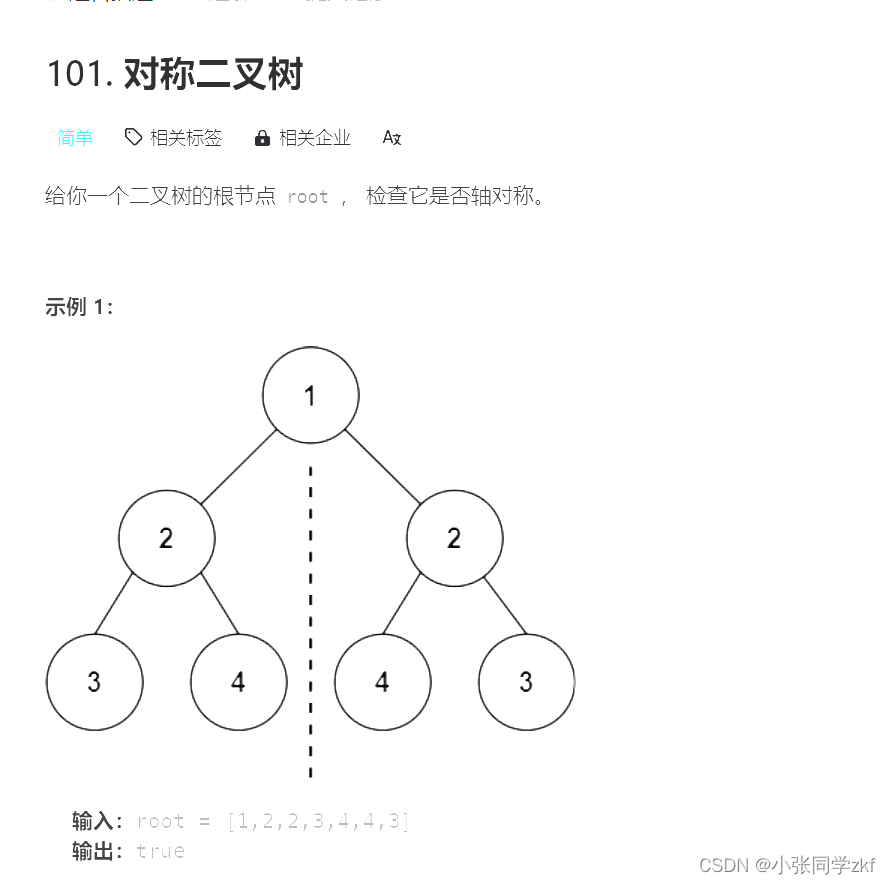
3.对称二叉树
这个对称二叉树就判断左子树与右子树是否相等就行了,也就是说把根节点的左右子树放到上面那道题函数里判断就行了
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) {return isSameTree(root->left,root->right);
}注意一下,这里要看左子树与右子树比较是否相等 ,所以传参的时候注意下
4.二叉树的前序遍历
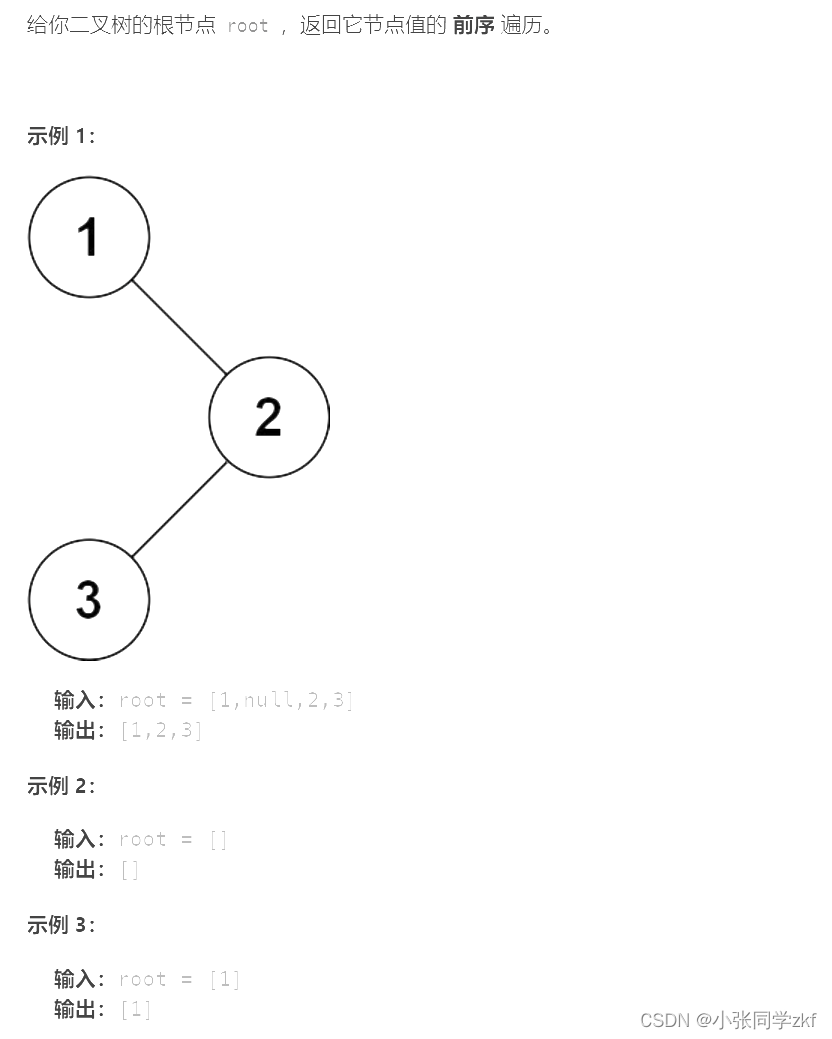
前序遍历我们上篇博客说过,但是这个前序遍历将所有根节点的数据,存储到数组中,以数组的形式返回,我们先开辟一个动态数组的空间, 将数组首地址与首下表,传入函数中,创建前序遍历函数,不过在此之前要统计一下二叉树的节点个数,得到数组里数据个数,然后通过递归将每个数据放入数组中,记得下标自增
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/int number(struct TreeNode* root){return root==NULL?0:number(root->left)+number(root->right)+1;}void preorder(struct TreeNode* root,int* a,int* pi){if(root==NULL)return;a[(*pi)++]=root->val;preorder(root->left,a,pi);preorder(root->right,a,pi);}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize=number(root);int* a=(int *)malloc(sizeof(int)*(*returnSize));int i=0;preorder(root,a,&i);return a;
}中序后序亦是如此
5.另一棵树的子树

相当于直接通过前序遍历把所有子树找到,然后依次导入我们上边说的判断两棵树是否相等的函数里就行了 ,前提俩子树数据相等
代码如下

结束语
典型的二叉树有关习题总结完了,二叉树主要是遍历,要想判断二叉树里什么什么的可能都得需要遍历,遍历那肯定需要递归,所以递归一定要弄明白
OK,本篇博客结束,感谢观看!!!