【线性代数】第一章 概率论的基本概念

一、随机试验

二、样本空间、随机事件

2.1 样本空间、样本点

• 随机试验 E 的所有可能结果组成的集合称为 E 的样本空间, 记为 S .
• 样本空间的元素 , 即试验E 的每一个结果, 称为样本点.

2.2 随机事件的概念

2.3 随机事件之间的关系及运算

• 包含关系

• A = B

• 事件 A 与 B 的并(和事件)

• 事件 A 与 B 的交 (积事件)

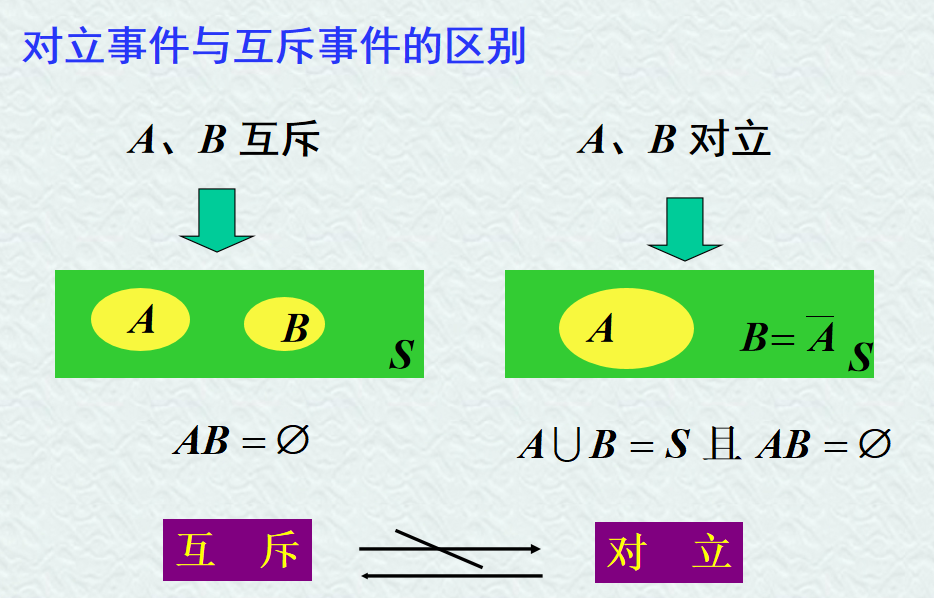
• 事件 A 与 B 互不相容 (互斥)

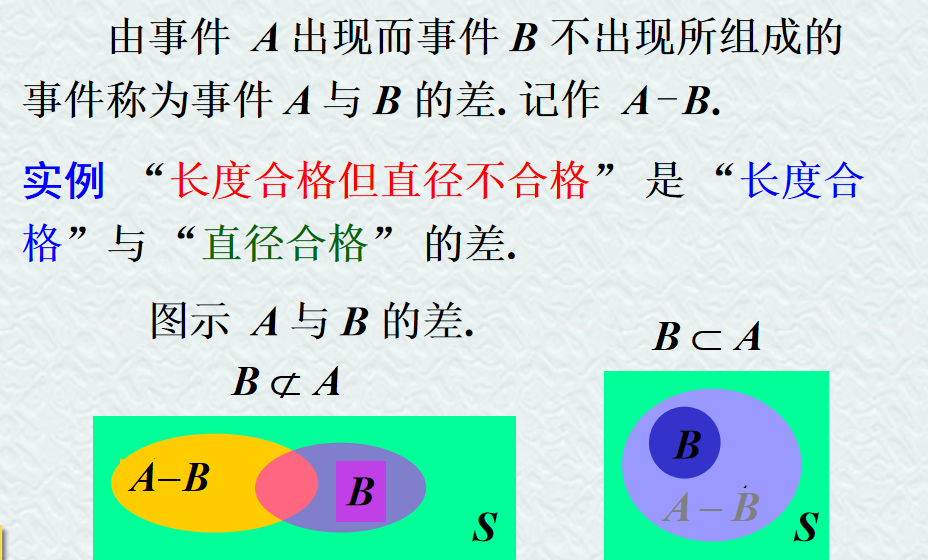
• 事件 A 与 B 的差
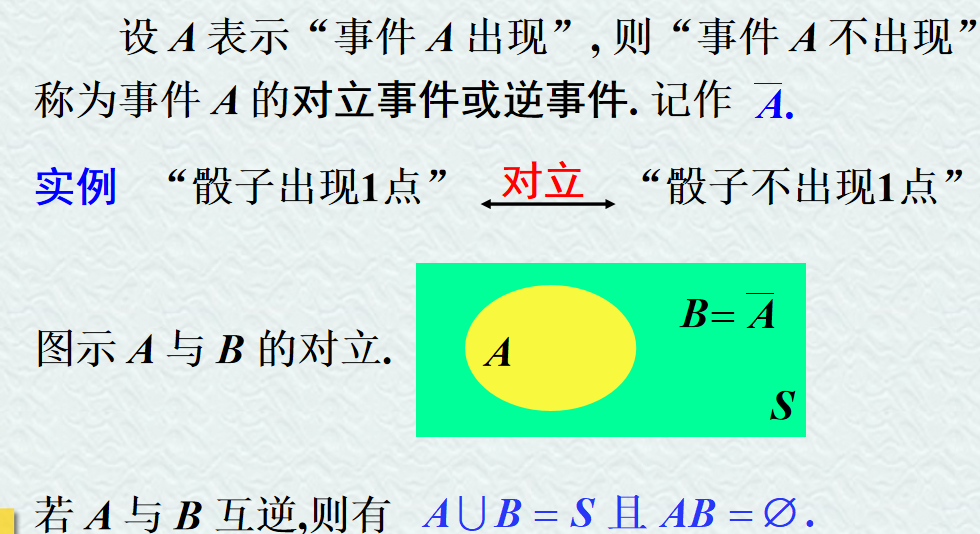
• 事件 A 的对立事件
  

事件之间的运算规律

三、频率与概率

3.1 频率的定义与性质

3.2 概率的定义与性质

概率的性质

四、等可能概型(古典概型)与几何概率

4.1 等可能概型(古典概型)

4.2 几何概型

五、条件概率

5.1 条件概率的定义

5.2 条件概率的性质

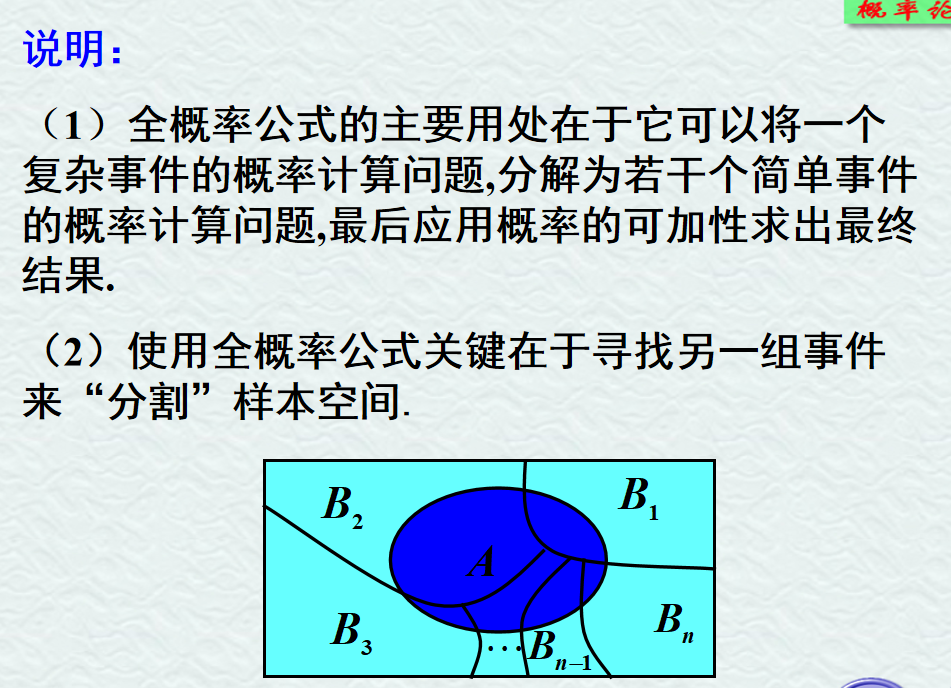
5.3 条件概率的三大公式

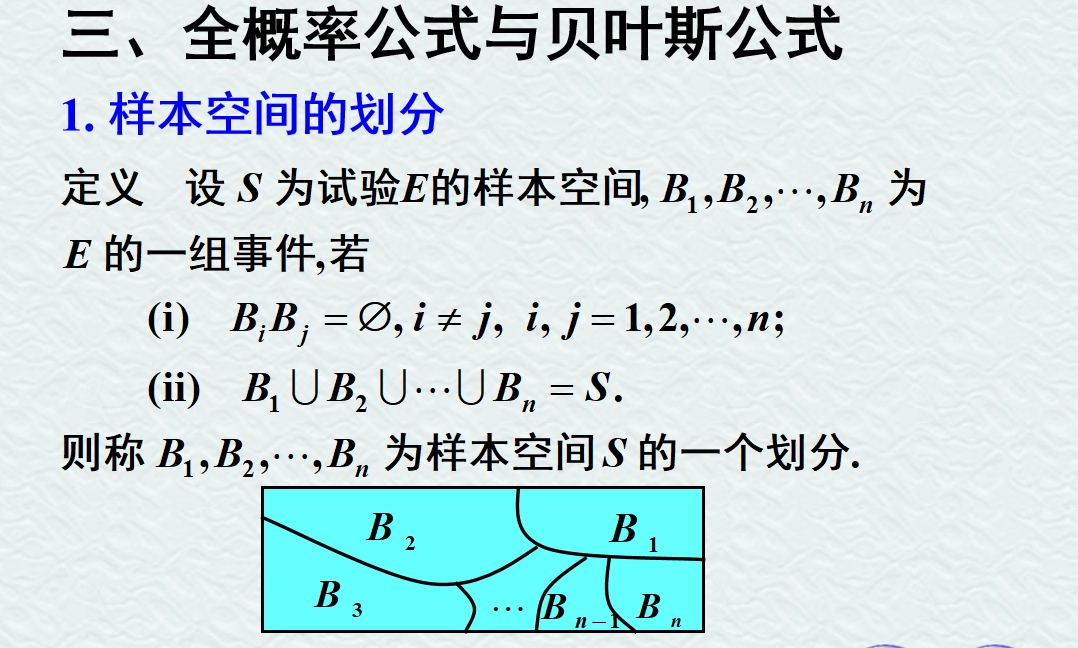
六、独立性

6.1 事件的相互独立性

6.2 几个重要的定理