1.红黑树的概念
红黑树是一颗二叉搜索树,他的每一个结点增加一个存储位来表示结点的颜色,可以是红色或者黑色,其中会有四条规则对红黑树进行约束,以下我将一一介绍.
1.1 红黑树的规则:
1.每个结点不是红色就是黑色
2.根结点是黑色的
3.如果一个结点是红色的,则它的两个孩子结点必须是黑色的,也就是说任意的一条路径不会有连续的红色结点。
4.对于任意一个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的黑色结点
以下的图为一个标准的红黑树:

1.2 如何确保红黑树满足规则4?
1.由规则4可知各个路径要有相同的黑色结点数量,所以在极端的情况下,最短的路径可以全是黑色结点,假设这个路径的黑色结点为bh(black height)
2.由规则2和3可知,任意一条路径不会有连续的红色结点出现,所以是红色和黑色结点交替出现,此时最长的路径的高度为2*bh.
3.综合红黑树的4条规则可以知道,一个正常的红黑树任意一条路径的高度h,满足bh<=h<=2*bh
1.3 红黑树的效率
假设N是红黑树中结点的数量,h是最短路径的长度, ,由此推出h约等于logN,那么时间复杂度还是O(logN)。
,由此推出h约等于logN,那么时间复杂度还是O(logN)。
2.红黑树的实现
2.1 红黑树的结构
enum Colour
{
RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{
pair<K,V>_kv;
RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}};template<class K,class V>class RBTree{typedef RBTreeNode<K,V> Node;public:private:Node*_root = nullptr;};
2.2 红黑树的插入
2.2.1 红黑树插入一个值的大概过程
1.插入一个值按二叉搜索树规则进行插入,插入后我们只需要观察是否符合红黑树的4条规则。
2.如果是空树插入,新增结点是黑色结点。如果是非空树插入,新增结点必须为红色结点,因为如果插入的是黑色结点会破坏规则4。
3.如果插入的父亲结点为黑色结点就没有违反任何规则,插入就会结束。
4.如果插入的父亲结点为红色的,则违反规则3,要进一步变化,在这里先把新增的结点叫做cur(缩写为c),c的父亲结点为parent(缩写为p),p的父亲标识为grandfather(缩写为g),p的兄弟叫做uncle(缩写为u)。
2.2.2 情况1:变色
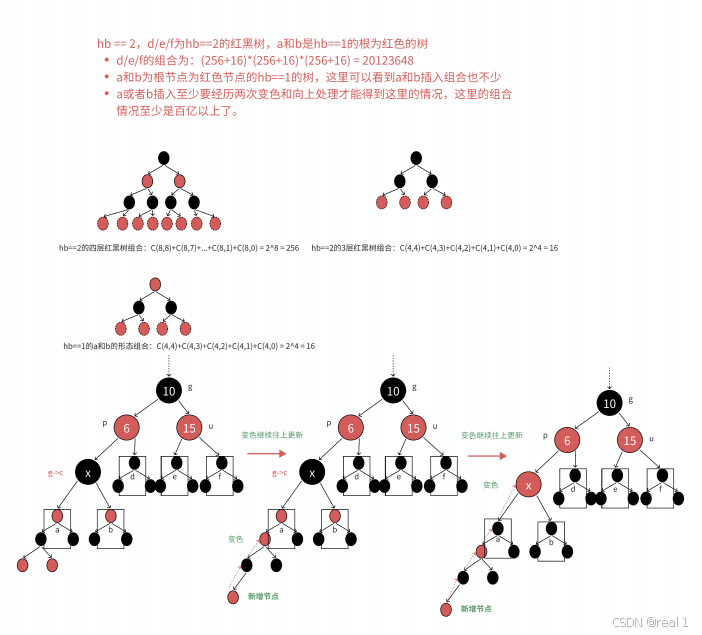
c为红,p为红,g为黑,u存在且为红,则将p和u变黑,g变红,再把g当做新的c,继续往上更新。(这样既不会有两个连续的红色结点,也能让两个路径的黑色结点数量相等,从而满足规则4)
如下图所示:

红黑树跟前面我发布的C++之AVL树类似有,还有很多情况,这里就不一一介绍,按照上述的思维即可理解:



 2.2.3 情况2:单旋+变色
2.2.3 情况2:单旋+变色
c为红,p为红,g为黑,u不存在或者u存在且为黑,u不存在,则c一定是新增结点,u存在且为黑,则c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。(关于是否为新增结点要根据路径黑色结点数量来判断)
分析:

p必须变黑才能解决两个红色结点连续的问题,u不存在或者是黑色,在p变成黑色,g变成红色后都无法满足红黑树的规则,所以这里除了变色还需要旋转。旋转在上篇文章:C++之AVL树已经介绍过了,这里的旋转跟AVL树的旋转类似。
这里分为两种情况:
1.

如果p是g的左,c是p的左,那么以g为旋转点进行右单旋再把p变黑,g变红即可。
2.

如果p是g的右,c是p的右,那么g为旋转点进行左单旋,再把p变黑,g变红即可。

2.2.4 情况3:双旋+变色
c为红,p为红,g为黑,u不存在或者u存在且为黑,u不存在,则c一定是新增结点,u存在且为黑,则c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
这里的双旋和变色又可以分为两种情况:
情况1:

如果p是g的左,c是p的右,那么先以p为旋转点进行左单旋,再以g为旋转点进行右单旋,再把c变黑,g变红即可。
情况2:

如果p是g的右,c是p的左,那么先以p为旋转带你进行右单旋,再以g为旋转点进行左单旋,再把c变黑,g变红即可。

2.3 红黑树的插入代码实现
bool Insert(const pair<K,V>&kv)
{
if(_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node*parent = nullptr;
Node*cur = _root
while(cur)
{
if(cur->_kv.first<kv.first)
{
parent = cur;cur = cur->_right;
}
else if(cur->_kv.first >kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur ->_col = RED;
if(parent->_kv.first < kv.first)
{
parent->_right = cur;}
else if(parent->_kv.first<kv.first)
{
parent->_left = cur;
}
cur->_parent = parent;
while(parent&&parent->_col == RED)
{
Node*grandparent = parent->_parent;
if(parent == grandfather->_left)
{
Node*uncle = grandfather->_right;if(uncle && uncle->_col == RED)
{
// u存在且为红-》变色再继续
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
}
else
{
// u存在且为黑或不存在-》旋转+变色
if(cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK ;grandfather->_col = RED;}else{//双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node*uncle = grandfather->_left;// 叔叔存在且为红, - 》变⾊即可if(uncle && uncle->_col == RED)if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为⿊{// 情况⼆:叔叔不存在或者存在且为⿊// 旋转 + 变⾊// g// u p// cif (cur == parent->_right){RotateL (grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR (parent);RotateL (grandfather);cur->_col = BLACK;grandfather->_col = RED;}break ;}}}_root->_col = BLACK;return true ;}
